Question

General solution of \[\tan 5\theta = cot2\theta \]
 A. \[\theta = \dfrac{{n\pi }}{7} + \dfrac{\pi }{{14}}\]
B. \[\theta = \dfrac{{n\pi }}{7} + \dfrac{\pi }{5}\]
C. \[\theta = \dfrac{{n\pi }}{7} + \dfrac{\pi }{2}\]
D. \[\theta = \dfrac{{n\pi }}{7} + \dfrac{\pi }{3}\]

Answer 1

Hint: Using the knowledge that the answer to the equation \[tan{\rm{ }}x = tan\] is given by \[x = n + \]for any arbitrary integer n, we apply the complementary angle relation \[tan = cot\left( 2 \right)\]to convert the cotangent in the preceding equation \[tan{\rm{ }}5 = cot{\rm{ }}2\]to tangent and then discover the solution.

Complete step by step solution:
 
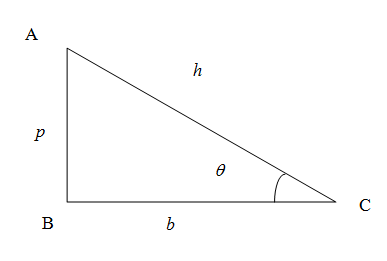
We are aware that in a right-angled triangle, the horizontal side is known as the base and is denoted by the letter \[b\]. The vertical side is known as the perpendicular and is denoted by the letter \[p\].
Here, in the right-angled triangle ABC figure above, we have:
\[AC = h,AB = p,BC = b\]
We can infer from trigonometric ratios that the opposite side to the adjacent side (excluding the hypotenuse, also known as leg adjacent) is the tangent of a right-angled triangle. As a result, we have the angle's tangent \[\theta \].
\[tan\theta = ABAC = pb\]
The term "co-tangent" refers to the ratio of the leg next to the opposing side, which is indicated by the symbol \[\cot \theta \] and is provided by
\[cot\theta = AC/AB = bp\]
We are aware that a triangle's total number of angles is \[180 \circ \]. Thus, we have
\[A + B + C = {180^ \circ }\]
\[ \Rightarrow A + C = {90^ \circ }\]
\[ \Rightarrow A = {90^ \circ } - C = {90^ \circ } - \theta \]
For angles A and C, we apply the definitions of tangent and cotangent,
\[tanC = tan\theta = pb,cotC = cot\theta = bp\]
\[cotA = cot(90 - \theta ) = pb,cotA = cot(90 - \theta ) = bp\]
\[tan(90 \circ - \theta ) = cot\theta ,cot(90 \circ - \theta ) = sin\theta \]
The above mentioned formula is also known as the tangent-cotangent reduction formula or complementary angle relation of tangent and cotangent.
We are aware of the solutions to the equation \[\tan x = \tan \alpha \], where x is the unknown and \[\alpha \] is the known angle.
\[x = n\pi + \alpha \]
The trigonometric equation with an unknown angle is provided in the question as,
\[tan5\theta = cot2\theta \]
\[ \Rightarrow tan5\theta = tan(90 \circ - 2\theta )\]
\[ \Rightarrow tan5\theta = tan(\pi /2 - 2\theta )\]
\[\alpha = \dfrac{\pi }{2} - 2\theta \]
\[ \Rightarrow 5\theta = n\pi + \pi /2 - 2\theta \]
\[ \Rightarrow 7\theta = n\pi + \pi /2\]
To get the desired outcome, we divide the aforementioned calculation by seven.
\[ \Rightarrow \theta = n\pi /7 + \pi /14,n \in Z\]

Option ‘A’ is correct

Note: The given result is well defined because the tangent function is not defined for \[\theta = \left( {2n + 1} \right)\dfrac{\pi }{2}\]and the cotangent function is not defined for\[\theta = n\pi \]. The complimentary and supplementary angle relations, which are determined by a shift of radians, must not be confused.\[\tan \left( {\pi + \theta } \right) = - \tan \theta ,\cot \left( {\pi + \theta } \right) = - \cot \theta \].