Question

Four point masses, each of mass M are placed at corner of square ABCD of side L. The moment of inertia of this system about an axis passing through A and parallel to BD is
(A) $3M{L^2}$
(B) \[M{L^2}\]
(C) $2M{L^2}$
(D) $\sqrt 3 M{L^2}$

Answer 1

Hint: Since each corner of square ABCD has a mass and we need to find the inertia parallel to BD so we will be using the parallel axis theorem.
Formula Used:
\[I = {I_{cm}} + M{a^2}\]

Complete step by step answer
First, we will draw the diagram. Here, OP is the perpendicular drawn from O to AD. XX’ is drawn passing through A and parallel to BD. The length of AP and AD to be equal as $\dfrac{L}{2}$.
         
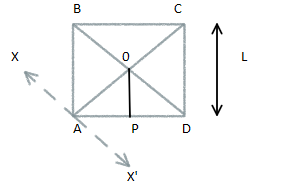
We know from properties of square that $\angle BAD = {90^0}$, so $\angle OAP = {45^0}$. To get OA, \[\cos {45^0} = \dfrac{{L/2}}{{AO}} \Rightarrow AO = \dfrac{L}{{2\cos {{45}^0}}} = \dfrac{L}{{2 \times 1/2}} = \dfrac{L}{{\sqrt 2 }}\].
To find moment of inertia at A, we will apply parallel axis theorem, \[I = {I_{cm}} + M{a^2}\]where
${I_{cm}}$is the moment of inertia at center of mass, M is the mass a be the distance between two axes.
\[{I_{XX'}} = {I_{cm}} + M{(AO)^2}\]
The moment of inertia at center will be because of all four points A, B, C, D.
So \[{I_{XX'}} = ({I_A} + {I_B} + {I_C} + {I_D}) + M{(AO)^2} = M{(\dfrac{L}{{\sqrt 2 }})^2} + 0 + M{(\dfrac{L}{{\sqrt 2 }})^2} + 0 + 4M{(\dfrac{L}{{\sqrt 2 }})^2}\]
\[ \Rightarrow {I_{XX'}} = \dfrac{{M{L^2}}}{2} + \dfrac{{M{L^2}}}{2} + \dfrac{{4M{L^2}}}{2} = 3M{L^2}\]

Correct answer is A. $3M{L^2}$

Additional information

There are basically two theorems used in calculating moment of inertia. They are –
Parallel Axis Theorem which states that a body’s moment of inertia about any axis is the sum of moment of inertia about a parallel axis which passes through the center of mass and the product of mass of body and perpendicular distance between axes square.
Perpendicular Axis Theorem which says that a body’s moment of inertia about a perpendicular to plane axis is the sum of moment of inertia of any two-perpendicular axis in the first axis intersecting plane.

Note
Moment of inertia at point B and D is zero as the perpendicular distance for both the points are zero.