Question

For given uniform square lamina ABCD, whose centre is O, which of the following is correct?

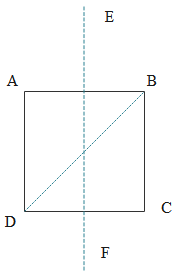
(A) $\sqrt {{{21}_{AC}}} = {1_{EF}}$
(B) ${I_{AD}} = {31_{EF}}$
(C) ${I_{AD}} = {I_{EF}}$
(D) ${I_{AC}} = \sqrt {{{21}_{EF}}}$

Answer 1

Hint The moment of inertia is defined to be a quantity which expresses a body’s tendency to the resist angular acceleration, which is known as the sum of the products of the mass of each of the particle in the body with the square of the distance from the axis of rotation. Based on this concept we can solve this question.

Complete step by step answer:
We know that the moment of inertia of a square lamina about an axis perpendicular to its plane = $\dfrac{{m{l^2}}}{6}$
Therefore, by perpendicular axes theorem,
${21_{EF}} = \dfrac{{m{l^2}}}{6} \to {I_{EF}} = \dfrac{{m{l^2}}}{{12}}$
Similarly,
${21_{AC}} = \dfrac{{m{l^2}}}{6} \to {I_{AC}} = \dfrac{{m{l^2}}}{{12}}$
${I_{AC}} = {I_{EF}}$

Hence, the correct answer is Option A.

Note The concept of moment of inertia is important because all the physics problems that involve all the masses in the rotational motion. It will be used to calculate the angular momentum and allows us to explain. This explanation is done using the conservation of the angular momentum. If we increase the radius of the axis of rotation, the moment of inertia increases. This will result in the lowering of the speed of rotation.