Question

For a particle projected in a transverse direction from a height above Earth’s surface, find the minimum initial velocity so that it just grazes the surface of the Earth such that the path of this particle would be an ellipse with center of the Earth as the farther focus, point of projection.

Answer 1

Hint: Here we have to make the particle travel around the earth’s orbit in a circular motion. To do so there are two conservation laws that need to be applied. These are the law of angular momentum conservation and law of energy conservation. Apogee is the farthest distance from the earth of the particle and perigee is the nearby distance from the earth to the particle. We have to consider apogee and perigee points to make the particle go around the earth’s orbit. After that, define a relation between them and find the velocity in the given question.

Formula Used:
Here we apply Conservation of momentum and conservation of energy as follows.
$mv(R + h) = m{v_1}R$ (Conservation of angular momentum)
M = mass;
R = Radius;
R+h = Total height from the center of the earth to Apogee.
v = velocity of satellite or object
${v_1}$= velocity of Earth.
Similarly
\[ - G\dfrac{{Mm}}{{(R + h)}} + \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{v_1}^2 + G\dfrac{{Mm}}{{(R)}}\] (Conservation of energy)
Where
G = Gravitational constant
M= mass of the object.
R = Radius
R+h = Total height from the center of the earth to Apogee.

Complete step by step answer:
Step 1: Apply the conservation of momentum and conservation of energy.

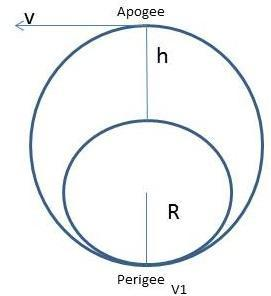
Here, the angular momentum is conserved as there is no net external torque acting on the system.
$mv(R + h) = m{v_1}R$ (Conservation of angular momentum) …(1)
Here the total energy of the system is equal to potential energy and kinetic energy of the system, also here the gravitational force of the earth is acting on the particle and we know that the gravitational force is an internal force, so the net total mechanical energy of the system is conserved.
E = P.E+K.E;
\[P.E = - G\dfrac{{Mm}}{{(R + h)}}\];
\[K.E = \dfrac{1}{2}m{v^2}\];
Here we are taking the potential energy from the Apogee (R+h).
$\implies$ \[ - G\dfrac{{Mm}}{{(R + h)}} + \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{v_1}^2 + G\dfrac{{Mm}}{{(R)}}\] (Conservation of energy) ….(2)
Solve equation (1) for ${v_1}$
${v_1} = \dfrac{{v(R + h)}}{R}$. …(3)
$\implies$ \[ - G\dfrac{{Mm}}{{(R + h)}} + \dfrac{1}{2}{v^2} = \dfrac{{{v^2}}}{2}\dfrac{{{{(R + h)}^2}}}{{{R^2}}} - \dfrac{{GM}}{R}\] ….(4)
Solve LHS and RHS and take common
$\implies$ \[GM(\dfrac{1}{R} - \dfrac{1}{{(R + h)}}) = \dfrac{{{v^2}}}{2}(\dfrac{{{{(R + h)}^2}}}{{{R^2}}} - 1)\] ….(5)
Solve and simplify the above equation
$\implies \dfrac{{GMh}}{{R(R + h)}} = \dfrac{{{V^2}}}{2}(\dfrac{{{R^2} + {h^2} + 2RH - {R^2}}}{{{R^2}}})$ ………(6
$\implies \dfrac{{GMh}}{{R + h}} = \dfrac{{{V^2}}}{2}({h^2} + 2Rh)$ …..(7)
Cancel out the “h” from both the sides.
$\implies \dfrac{{GM}}{{R + h}} = \dfrac{{{V^2}}}{2}(h + 2R)$ …..(8)
$\implies$ \[\dfrac{{GM}}{{(R + h)(h + 2R)}} = \dfrac{{{V^2}}}{2}\] …(9)
Transfer the square from and put square root on the LHS
$\implies$ \[\sqrt {\dfrac{{GM}}{{(R + h)(h + 2R)}}} = \dfrac{V}{2}\] …(10)
Now, for Earth’s surface (r = R+h).
$\implies$\[\sqrt {\dfrac{{2GM}}{{r(r + R)}}} = V\] ……(11)

Final Answer: The minimum initial velocity so that it just grazes the surface of the Earth such that the path of this particle would be an ellipse with center of the Earth as the farther focus, point of projection is
\[\sqrt {\dfrac{{2GM}}{{r(r + R)}}} = V\]

Note: Make sure to go step by step. Make proper use of the conservation laws (angular momentum and energy) and apply it very carefully in the question. Make proper relation with both of the conservation laws and make suitable deductions and find out the initial velocity.