Question

Find the vertex connectivity of any tree.
A. One
B. Two
C. Three
D. None of the above

Answer 1

Hint: First recall the definition of vertex connectivity of a tree and the definition of a tree, then answer the given question.

Complete step by step solution:
The vertex connectivity of a graph G is the minimum number of vertices whose removal disconnects G.
Now, a tree is an undirected connected graph in which two vertices are connected by exactly one path.
For example let us draw a tree,

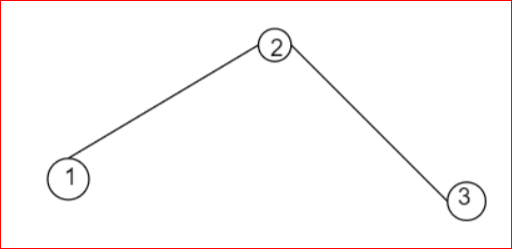
Image: Tree
Now, from the image we can see that if we remove the edge of vertex 1 and 2 then the graph becomes disconnected also if we remove the edge of vertex  2 and 3 this also makes the graph disconnected. 
Therefore, the removal of one vertex makes the graph disconnected.
Hence, the vertex connectivity of a tree is always one.

The correct option is A.

Note: Sometimes students draw a tree and shows that when they remove one vertex the graph got disconnected. This is also a good approach to answer this question.
For example, 

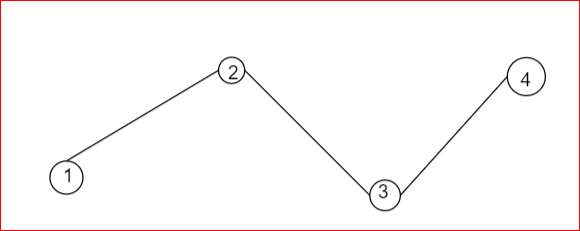
Image: Tree
This diagram is of a tree.
But, if we remove any one edge, suppose we are removing the edge of the vertices 1, 2. Then the graph becomes

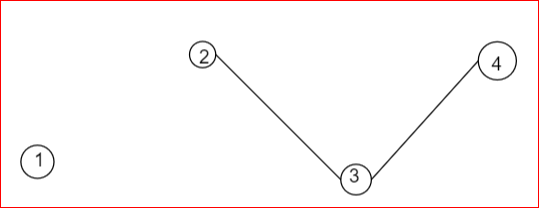
Image: Tree
This is not a connected graph, therefore this is not a tree.
Hence, the vertex connectivity of a tree is 1.