Question

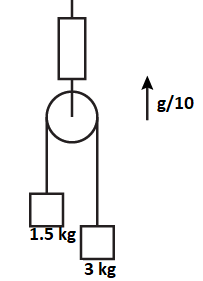
Find the reading of the spring balance shown in figure. The elevator is going up with an acceleration of g/10, the pulley and the string are light and the pulley is smooth.

Answer 1

Hint: For every pulley and the string system question, try to draw a free body diagram (FBD) for the given situation and then with the help of FBD, write relevant equations involving all the forces acting on the body and solve them.

Complete step by step solution:
Given that the elevator is going up with an acceleration of g/10.
Free body diagram (FBD) is a diagram showing all forces acting on a body using arrows, considering body as a point mass.
FBD of the given situation is shown below:

Tension (T): It is an internal molecular force which appear in a string when it is taunt by some external force. Force of tension always acts along the length of the string. Force of tension always act along the length of the string. Direction of tension is always away from the tied ends or points of contact of string. It always has pulling tendency.

Here, $\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}$ and $\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}$are pseudo force.
Let us consider that mass of body A is 3 kg and mass of body B is 1.5 kg (as per given figure)
For body A
${{{m}}_{{A}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}...{{(i)}}$
For body B
${{{m}}_{{B}}}{{a = }}{{{m}}_{{B}}}{{g + }}\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}{{ - T}}...{{(ii)}}$
Adding equations (i) and (ii), we get
$
  {{{m}}_{{A}}}{{a + }}{{{m}}_{{B}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}{{ + }}{{{m}}_{{B}}}{{g + }}\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}{{ - T}} \\
   \Rightarrow {{(}}{{{m}}_{{A}}}{{ + }}{{{m}}_{{B}}}{{)a = (}}{{{m}}_{{B}}}{{ - }}{{{m}}_{{A}}}{{)g + (}}{{{m}}_{{B}}}{{ - }}{{{m}}_{{A}}}{{)}}\dfrac{{{g}}}{{{{10}}}} \\
$
As ${{{m}}_{{A}}}{{ = 1}}{{.5 kg}}$ and ${{{m}}_{{B}}}{{ = 3 kg}}$
On substituting the values of masses ${{{m}}_{{A}}}$and ${{{m}}_{{B}}}$in above equation, we get
$
  {{(1}}{{.5 + 3)a = (3 - 1}}{{.5)g + (3 - 1}}{{.5)}}\dfrac{{{g}}}{{{{10}}}} \\
   \Rightarrow 4.{{5a = 1}}{{.5g - 1}}{{.5}}\dfrac{{{g}}}{{{{10}}}} \\
   \Rightarrow {{4}}{{.5a = 1}}{{.5g}}\left( {{{1 - }}\dfrac{{{1}}}{{{{10}}}}} \right) \\
   \Rightarrow {{4}}{{.5a = 1}}{{.5g \times }}\dfrac{{{9}}}{{{{10}}}} \\
  \therefore \dfrac{{{a}}}{{{g}}}{{ = }}\dfrac{{{3}}}{{{{10}}}} \\
$
Now using equation (i), we get
$
  {{{m}}_{{A}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}} \\
  {{Or }} \\ T= {{{m}}_{{A}}}{{(a + g + }}\dfrac{{{g}}}{{{{10}}}}{{)}} \\
$
Reading of the spring balance is given by
$
  \dfrac{{{{2T}}}}{{{g}}}{{ = }}\dfrac{{{2}}}{{{g}}}{{{m}}_{{A}}}{{(a + g + }}\dfrac{{{g}}}{{{{10}}}}{{)}} \\
  {{Or }} \\ \dfrac{{{{2T}}}}{{{g}}}{{ = 2 \times 1}}{{.5}}\left( {\dfrac{{{a}}}{{{g}}}{{ + 1 + }}\dfrac{{{1}}}{{{{10}}}}} \right) \\
   \Rightarrow {{3}}\left( {\dfrac{{{3}}}{{{{10}}}}{{ + 1 + }}\dfrac{{{1}}}{{{{10}}}}} \right){{ = 3(0}}{{.3 + 1 + 0}}{{.1) = 4}}{{.2 Kg}} \\
$

The reading of the spring balance will be 4.2 Kg.

Note: In free body diagram, we draw only those forces by arrows which are experienced by the body. We don’t draw those forces that are applied by the body or not acting on the body.