Question

Find the number of points in $\left( { - \infty ,\infty } \right)$ for which ${x^2} - x\sin x - \cos x = 0$ .
A. 6
B. 4
C. 2
D. 0

Answer 1

Hint: First rewrite the equation by adding $x\sin x + \cos x = 0$to both sides of the given equation. Then suppose that $f(x) = {x^2}$ and $g(x) = x\sin x + \cos x$. Then draw the graph of these two functions and obtain the number of points of intersections of these graphs.

Complete step by step solution:
Substitute -1, 0, 1, 2 for x in the function f(x) to obtain the corresponding coordinates.
Therefore, the points are $( - 1,1),(0,0),(1,1),(2,4)$ .
Plot these points on the graph and join them by a smooth curve to obtain the graph of f(x).
Substitute -1, 0, 1, 2 for x in the function g(x) to obtain the corresponding coordinates.
Therefore, the points are $( - 1,0.9),(0,1),(1,0.9),(2,1.6)$ .
Plot these points on the graph and join them by a smooth curve to obtain the graph of g(x).
The required graph is,

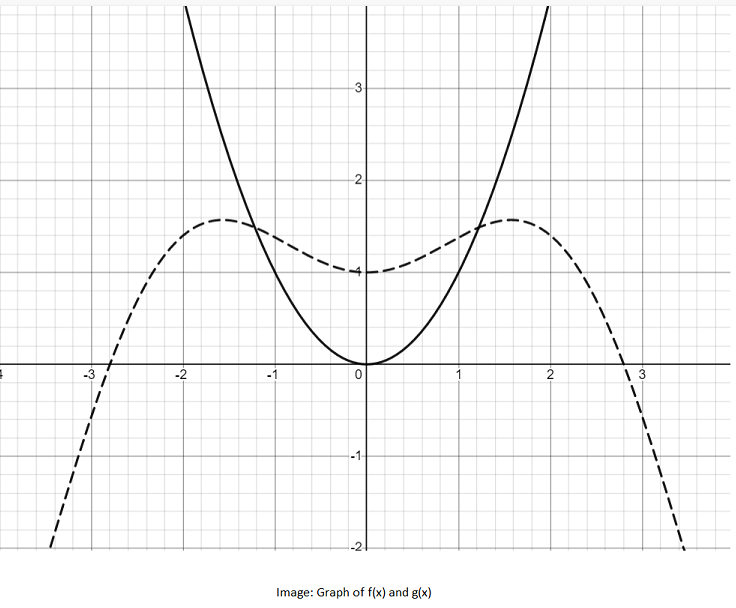
The graph of f(x) is in solid line and the graph of g(x) is in dotted line.
So, we can see the number of points of intersection of f(x) and g(x) are 2.

Option ‘C’ is correct

Note: In the above solution, we used the term "function," which can be defined as a relationship between the provided inputs and their outputs, such that each input is directly related to one output.