Question

Find the locus of the point which moves so that its distance from x-axis is double of its distance from y-axis.
A. $x = 2y$
B. $y = 2x$
C. $y = 2x + 3$
D. $x = 5y + 1$

Answer 1

Hint: Draw a diagram of the stated problem and mark the given information, Then obtain the required relation with the help of the obtained diagram.

Complete step by step solution:
The diagram of the given problem is,

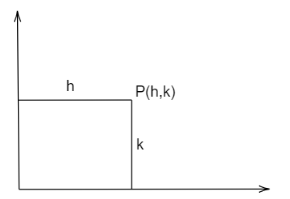
Image: Point P(h,k)

From the diagram we can see that the distance from the x-axis is k and y-axis is h.
It is given that, distance from the x-axis is double of its distance from the y-axis.
Hence,
$k = 2h$ .
Therefore, the required locus is $y = 2x$

Option ‘B’ is correct

Additional information:
Locus of a point is a set of points that satisfy an equation of curve. The curve may be a circle or hyperbola or ellipse or a line etc.
In the given question, we get a linear equation.
If the equation of a locus of a point is linear, then the locus of the point represents a line.

Note: The distance of a point from the x-axis is the ordinate of the point. The distance of a point from the y-axis is the abscissa of the point. Using the concept, we will find the distance of the point from the x-axis and the y-axis. Then equate the ordinate of the point with 2 times the abscissa of the point. At the end of the solution, replace h with x and k with y.