
Find the length of the intercept, if the circle ${x^2} + {y^2} + 10x - 6y + 9 = 0$ is on the x-axis.
A. 2
B. 4
C. 6
D. 8
Answer
216.3k+ views
Hint: Firstly, we need to find the general equation of a circle and after that, we need to compare the given equation with the general equation of a circle. After getting to the center of the given circle. At last, we find the intercept of the circle by using the intercept formula of a circle.
Formula Used:
General equation of a circle is ${x^2}\; + \;{y^2}\; + \;2gx\; + \;2fy\; + \;c\; = \;0$ , where the center of a circle is $( - g, - f)$ and $c$ is a constant value.
Length of the intercept of the x-axis is $2\sqrt {{g^2} - c} $ unit.
Square root of a expression $a$ is $\sqrt {{a^2}} = a$
Complete step by step solution:
We draw the circle in graph
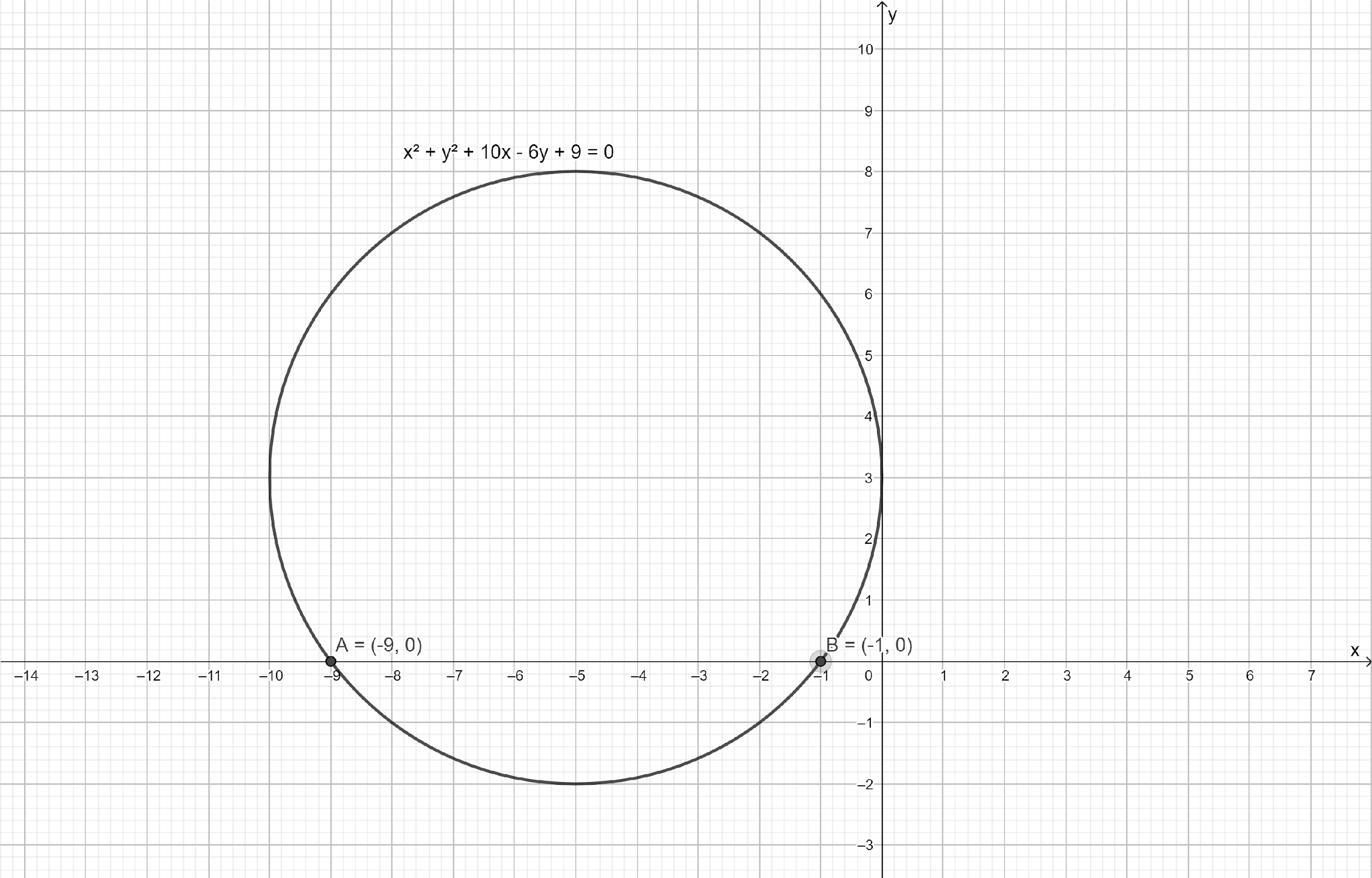
Image: Length of intercept $AB$ of the circle ${x^2} + {y^2} + 10x - 6y + 9 = 0$
Equating the given equation of circle ${x^2} + {y^2} + 10x - 6y + 9 = 0$ with the general equation of a circle ${x^2}\; + \;{y^2}\; + \;2gx\; + \;2fy\; + \;c\; = \;0$
We get the value of $g = 5,f = - 3$ and $c = 9$ .
Now we finding the length of x- intercept of the given circle
Using the x-intercept formula of a circle we get
$AB = 2\sqrt {{5^2} - 9} $
We know that ${5^2} = 25$ , substitute this and we get
$AB = 2 \times \sqrt {25 - 9} $
Subtracting and we get
$AB = 2 \times \sqrt {16} $
Using the square root and we get
$AB = 2 \times 4$
Multiplying and we get
$AB = 8$ unit
Therefore, the length of x intercept of the given circle is 8 units.
Option ‘D’ is correct
Note: Students often confuse the square root method. Some students write square root as $\sqrt {{a^2}} = \pm a$ , but in a square root method it always gives positive value. We need to take care of positive and negative signs while comparing the given equation with the general solution of a circle.
Formula Used:
General equation of a circle is ${x^2}\; + \;{y^2}\; + \;2gx\; + \;2fy\; + \;c\; = \;0$ , where the center of a circle is $( - g, - f)$ and $c$ is a constant value.
Length of the intercept of the x-axis is $2\sqrt {{g^2} - c} $ unit.
Square root of a expression $a$ is $\sqrt {{a^2}} = a$
Complete step by step solution:
We draw the circle in graph

Image: Length of intercept $AB$ of the circle ${x^2} + {y^2} + 10x - 6y + 9 = 0$
Equating the given equation of circle ${x^2} + {y^2} + 10x - 6y + 9 = 0$ with the general equation of a circle ${x^2}\; + \;{y^2}\; + \;2gx\; + \;2fy\; + \;c\; = \;0$
We get the value of $g = 5,f = - 3$ and $c = 9$ .
Now we finding the length of x- intercept of the given circle
Using the x-intercept formula of a circle we get
$AB = 2\sqrt {{5^2} - 9} $
We know that ${5^2} = 25$ , substitute this and we get
$AB = 2 \times \sqrt {25 - 9} $
Subtracting and we get
$AB = 2 \times \sqrt {16} $
Using the square root and we get
$AB = 2 \times 4$
Multiplying and we get
$AB = 8$ unit
Therefore, the length of x intercept of the given circle is 8 units.
Option ‘D’ is correct
Note: Students often confuse the square root method. Some students write square root as $\sqrt {{a^2}} = \pm a$ , but in a square root method it always gives positive value. We need to take care of positive and negative signs while comparing the given equation with the general solution of a circle.
Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions For Class 11 Maths Chapter 8 Sequences And Series

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses




