Question

Find the equivalent resistance of the given circuit:

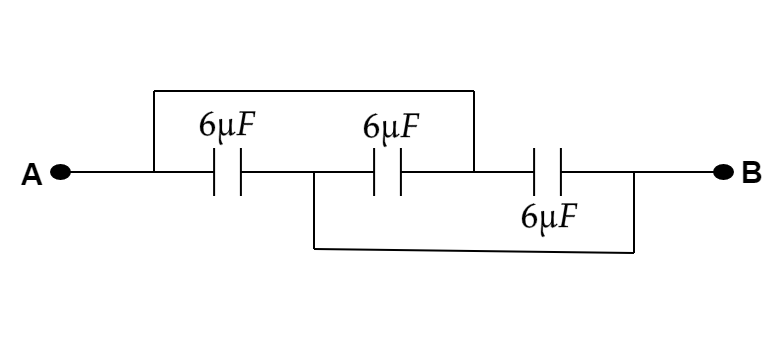
Answer 1

Hint: - In this question, first the equivalent circuit needs to be drawn between the given terminal points to identify whether the given capacitors are in series or in parallel. Now apply the formula of the series combination or the parallel combination to determine the equivalent capacitance.

Complete step-by-step solution:
In this problem, the circuit of the capacitance is known which has three capacitors and we need to determine the equivalent capacitance of the circuit.
The given circuit is,

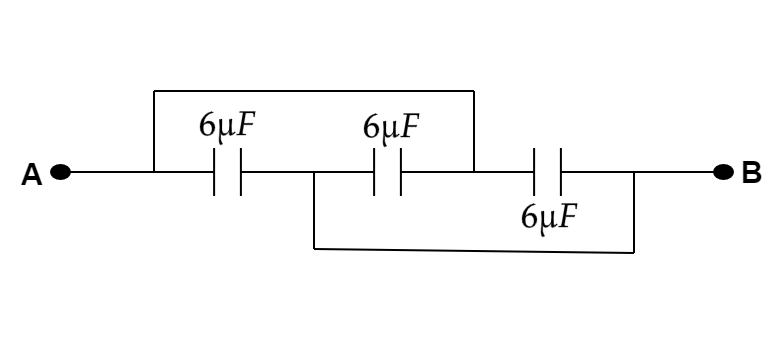
From the above diagram, we can see that the potential difference between each capacitor is the same, so all the capacitors between points A and B are in parallel. At this moment, we consider the equivalent circuit of the capacitor as,

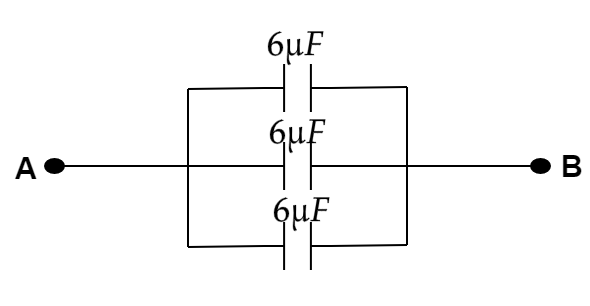
When capacitors are connected in parallel the equivalent capacitance, ${C_T}$ of the circuit is adequate to the sum of all individual capacitors connected.
By parallel connection of the capacitor equation, we will calculate the equivalent capacitance of the capacitor as,
${C_T} = 6 + 6 + 6$
After simplification, we get
$\therefore {C_T} = 18\mu F$

Thus, the equivalent capacitance of the capacitor between point A and B is $18\mu F$ .

Additional Information: We can define the capacitance as the ratio of the magnitude of the charge on either of the conductors to the magnitude of the potential difference between the two conductors. The unit of capacitance is Farad. There are two types of combinations possible in capacitor: parallel and series. The Series and parallel combination of capacitors have the opposite formula as that of resistance.

Note: We know that if the capacitors are in parallel then the equivalent capacitance of the capacitor is the sum of the individual capacitors but if the capacitors are in series then the capacitance of the capacitor is calculated by $\dfrac{1}{{{C_T}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$ . Where ${C_1}$ , ${C_2}$ , ${C_3}$ are the individual capacitance.