Question

Find the equivalent resistance between A and B (resistance of each resistor is R).

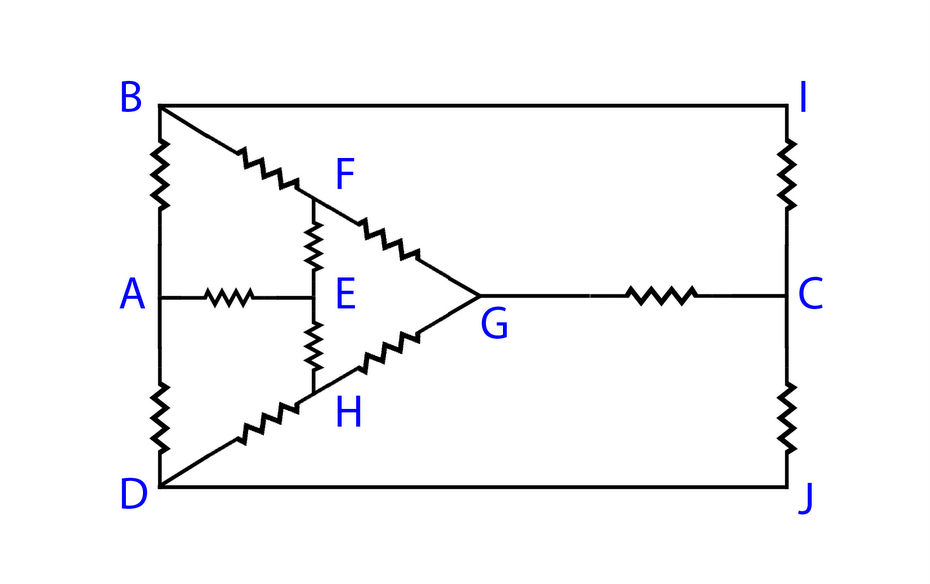
A) $\dfrac{7}{{12}}R$
B) $\dfrac{7}{{13}}R$
C) $\dfrac{7}{{15}}R$
D) $\dfrac{8}{{13}}R$

Answer 1

Hint:The problem is from the electricity part of physics. We can apply the concept of parallel combination and series combination of resistance here. Use the equation for effective resistance in parallel and series combinations.

Formula Used:
Equivalent resistance for a series resistance circuit:
${R_E} = {R_1} + {R_2} + {R_3}$
Where ${R_E}$= equivalent resistance and ${R_1},{R_2},{R_3}$ = component resistance.
Equivalent resistance for a parallel resistance circuit:
$\dfrac{1}{{{R_E}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Where ${R_E}$= equivalent resistance and ${R_1},{R_2},{R_3}$ = component resistance.

Complete answer:
The equivalent resistance is a single resistance which can replace all the component resistances in a circuit in such a manner that the current in the circuit remains unchanged.
The circuit can be re-draw into a simple form.

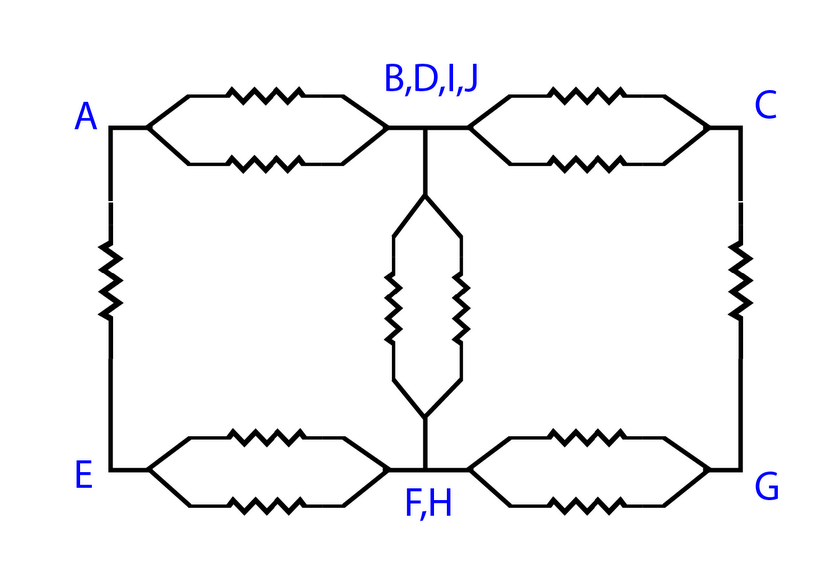
Now we can find the equivalent resistance for the five parallel combinations.
\[\dfrac{1}{{{R_E}}} = \dfrac{1}{R} + \dfrac{1}{R} = \dfrac{2}{R} \Rightarrow {R_E} = \dfrac{R}{2}\]
The circuit diagram will become.

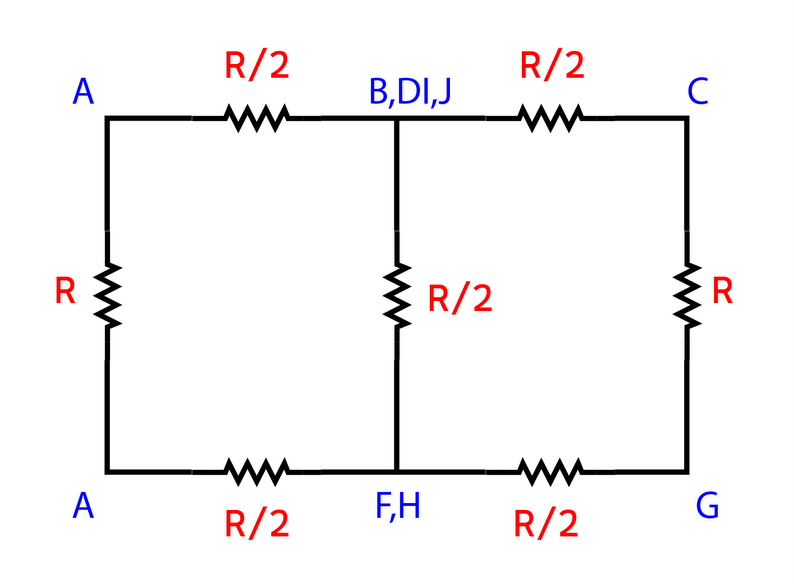
Three resistances in the right side are in series combination. Their equivalent resistance will become.
\[{R_E} = \dfrac{R}{2} + R + \dfrac{R}{2} = 2R\]
This equivalence resistance is in parallel with \[\dfrac{R}{2}\] on the right side.
\[\frac{1}{{{R_E}}} = \frac{1}{{2R}} + \frac{1}{\frac{R}{2}} = \frac{1}{{2R}} + \frac{2}{R} = \frac{5}{{2R}} \Rightarrow {R_E} = \frac{{2R}}{5}\]



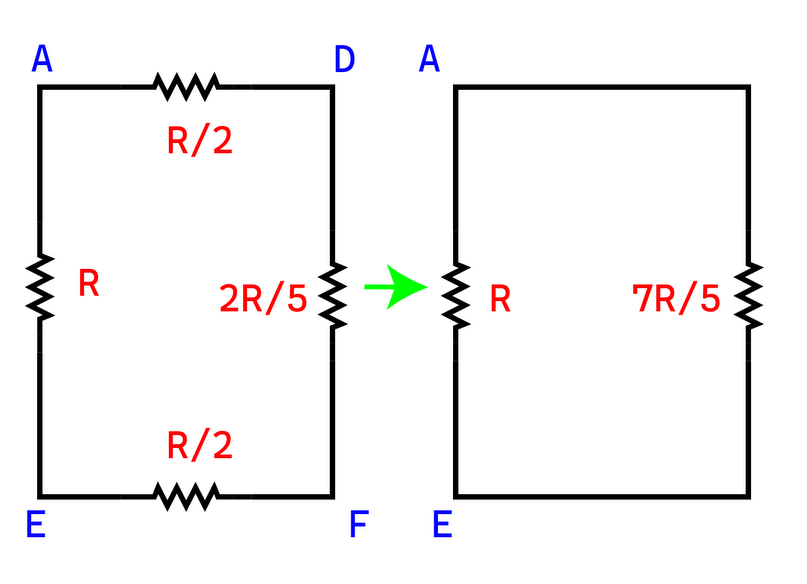
The three series combination resistance will be
\[{R_E} = \dfrac{R}{2} + \dfrac{R}{2} + \dfrac{{2R}}{5} = \dfrac{{7R}}{5}\]
The final parallel combination is solved by
\[\dfrac{1}{{{R_E}}} = \dfrac{1}{R} + \dfrac{1}{{\left( {\dfrac{{7R}}{5}} \right)}} = \dfrac{1}{R} + \dfrac{5}{{7R}} = \dfrac{{12}}{{7R}} \Rightarrow {R_E} = \dfrac{{7R}}{{12}}\]
Hence, the correct option is Option (A).



Note: Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance blocks the flow of current. The S.I unit of resistance is ohms. The current decreases as resistance increases. On the other hand, the current increases as the resistance decreases. While solving this question pay close attention to circuits and terminals in which these resistances are connected and apply the concepts of parallel combination and series combination of resistance accordingly.