Question

Find the equation of circle of radius 5 and touching the coordinate axes in third quadrant.
A. \[{\left( {x + 5} \right)^2} + {\left( {y + 5} \right)^2} = 25\]
B. \[{\left( {x - 5} \right)^2} + {\left( {y - 5} \right)^2} = 25\]
C. \[{\left( {x - 5} \right)^2} + {\left( {y + 5} \right)^2} = 25\]
D. \[{\left( {x + 5} \right)^2} + {\left( {y - 5} \right)^2} = 25\]

Answer 1

Hint: Draw a circle with the given conditions. Then write the general equation of a circle. Then substitute the required values of the centre and the radius obtained from the diagram and calculate to obtain the required result.

Formula used:
The general equation of a circle is,
\[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\]
Where, \[(h,k)\] is the centre and r is the radius.

Complete step by step solution:
The diagram of the given problem is,

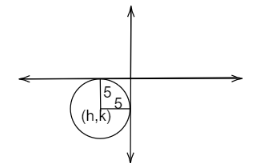
Image: Circle
From the diagram it is clear that the distance of the centre from the x-axis is 5 unit downward and the distance from the y-axis is 5 unit in the left direction.
Hence, the coordinate of the centre is \[( - 5, - 5)\] .
Therefore, the required equation is,
\[{\left( {x - ( - 5)} \right)^2} + {\left( {y - ( - 5)} \right)^2} = {5^2}\]
\[\therefore \]\[{\left( {x + 5} \right)^2} + {\left( {y + 5} \right)^2} = 25\]
The correct option is A.

Additional information:
In the first quadrant, ordinate and abscissa are positive integers. In the second quadrant, the abscissa of a coordinate is negative and the ordinate of a coordinate is positive. In the third quadrant, ordinate and abscissa of a coordinate both are negative. In the fourth quadrant, the abscissa of a coordinate is positive and the ordinate of a coordinate is negative.

Note: First draw the diagram for this type of question and then analyze it to compute the required results. From the diagram, it is very much clear that we shifted 5 units left and 5 units downward therefore the required centre is \[( - 5, - 5)\].