Question

Find the correct option
The maximum value of \[z = 10x + 6y\] subject to constraints \[x \ge 0\], \[y \ge 0\], \[3x + y \le 12\] and \[2x + 5y \le 34\] is
A.\[72\]
B.\[80\]
C.\[104\]
D.\[56\]

Answer 1

Hint: First, the graph of the feasible region solved by the given four inequalities represented as constraints is drawn and then the value of \[z\] is calculated at different boundaries of the region from which, the maximum value is found.

Complete step-by-step solution:We have been given the equation of the circle as \[z = 10x + 6y\] subject to constraints \[x \ge 0\], \[y \ge 0\], \[3x + y \le 12\] and \[2x + 5y \le 34\].
Let, \[{L_1}\]and \[{L_2}\]are two lines represented by the two equations \[3x + y = 12\]and \[2x + 5y = 34\]respectively.
Now, we will solve the above two equations.
Multiplying \[5\]with the equation \[3x + y = 12\]
\[15x + 5y = 60\]
Subtracting \[2x + 5y = 34\]from the equation \[15x + 5y = 60\], we have
\[15x + 5y - (2x + 5y) = 60 - 34\]
\[ \Rightarrow 15x + 5y - 2x - 5y = 26\]
\[ \Rightarrow 13x = 26\]
\[ \Rightarrow x = 2\]
Putting the value of \[x\] in the equation \[3x + y = 12\], we have
\[(3 \times 2) + y = 12\]
\[ \Rightarrow 6 + y = 12\]
\[ \Rightarrow y = 6\]
So, the two lines \[{L_1}\]and \[{L_2}\] intersect at the point \[B(2,6)\] and \[OABCO\]is the required feasible region as shown in the figure.

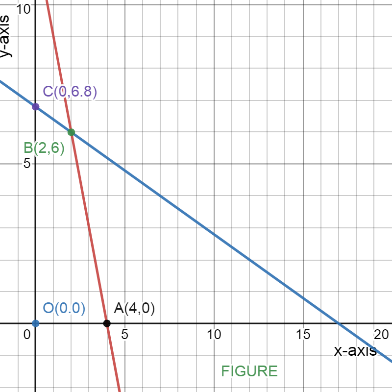
Image: Two lines intersecting

As shown in the figure, the point \[A\]of the region is the point, where, the line \[{L_1}:3x + y = 12\] intersects the X-axis.
Finding the co-ordinates of the point \[A\]
\[3x + y = 12\]
\[ \Rightarrow 3x = 12\] (Since \[y = 0\] on X-axis)
\[ \Rightarrow x = 4\]
So, the co-ordinates of the point \[A\] is \[(4,0)\].
The co-ordinates of the point \[B\] is \[(2,6)\], which is the intersection point of lines \[{L_1}\]and \[{L_2}\].
As shown in the figure, the point \[C\]of the region is the point, where, the line \[{L_2}:2x + 5y = 34\] intersects the Y-axis.
Finding the co-ordinates of the point \[C\]
\[2x + 5y = 34\]
\[ \Rightarrow 5y = 34\] (Since \[x = 0\]on Y-axis)
\[ \Rightarrow y = 6.8\]
So, the co-ordinates of the point \[C\] is \[(0,6.8)\].
The co-ordinates of the origin \[O\] is \[(0,0)\].
Now, we will calculate the value of \[z = 10x + 6y\]at the four points \[O,A,B\]and \[C\] of the region \[OABCO\]
At \[O(0,0)\], \[z = (10 \times 0) + (6 \times 0) = 0\]
At \[A(4,0)\], \[z = (10 \times 4) + (6 \times 0) = 40\]
At \[B(2,6)\], \[z = (10 \times 2) + (6 \times 6) = 56\]
At \[C(0,6.8)\], \[z = (10 \times 0) + (6 \times 6.8) = 40.8\]
So, the maximum value of \[z = 10x + 6y\]is \[56\]at the point \[B\].



Hence, the option D. \[56\] is the correct answer

Note: The solution set of a system of linear inequation in two variables is the set of all points \[(x,y)\], which satisfies all the inequations in the system simultaneously. So, the region of the plane common to all the portions comprising the solution sets of the given inequalities should be found. When, there is no region common to all the solutions of the given inequations, the solution set of the system is empty.