Question

Find \[A:B\] if A is the area bounded by the curve \[y = \sqrt {3x + 4} \], \[x - axis\] and the lines \[x = - 1\] and \[x = 4\] and B is the area bounded by curve \[{y^2} = 3x + 4\], \[x - axis\], and the lines \[x = - 1\]and \[x = 4\].
A. \[1:1\]
B. \[2:1\]
C. \[1:2\]
D. None of these

Answer 1

Hint: For A, we solve it by using substitution and then integrate using substitution. Also, curve B is nothing but the square of curve A, therefore, the answer will come out to be same.

Complete step by step solution

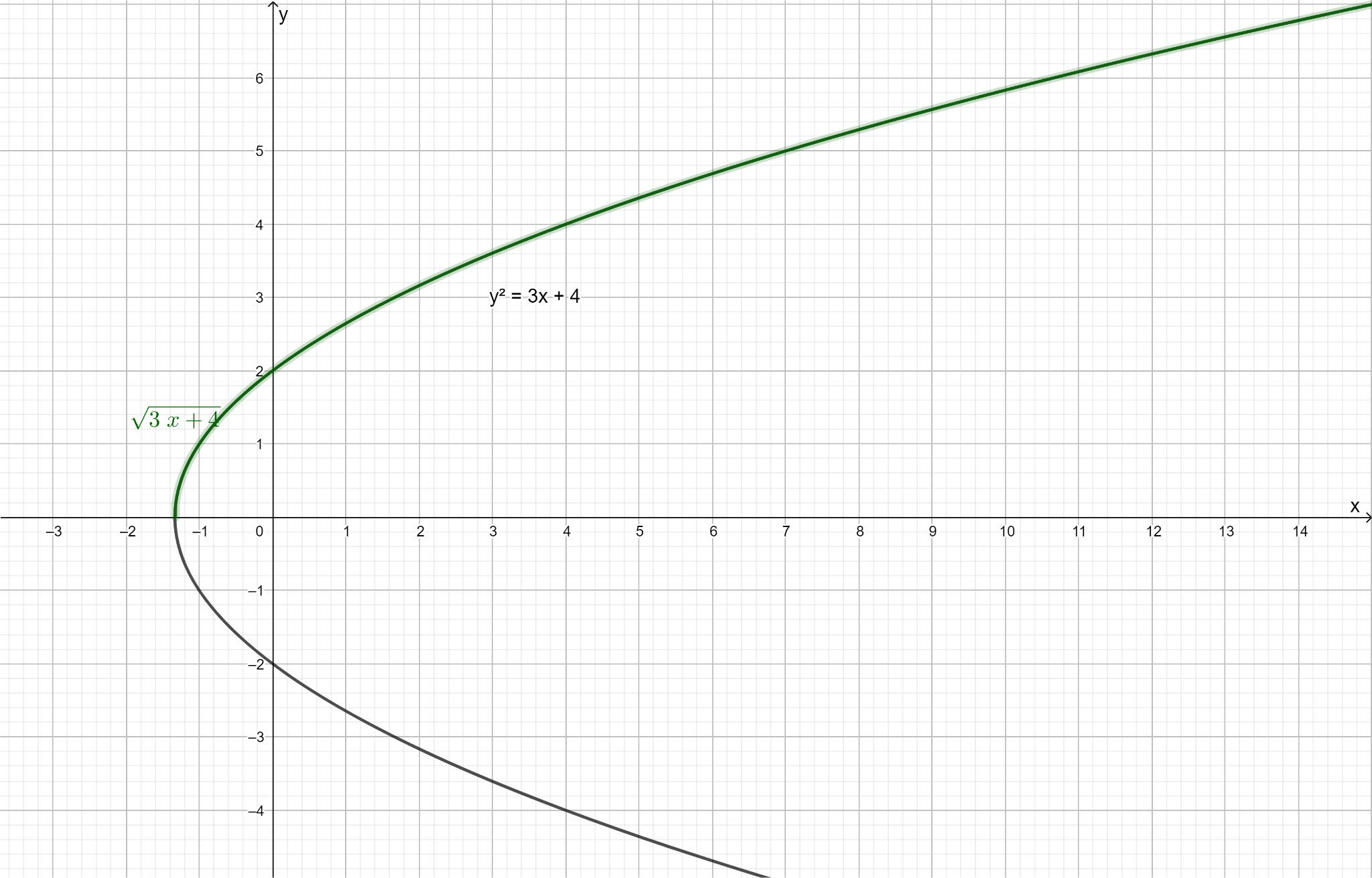
Image: Shown the path of \[y = \sqrt {3x + 4} \] and \[{y^2} = 3x + 4\] in graph paper
We have, first curve as:
\[y = \sqrt {3x + 4} \]
Now, A, area bounded by the curve will be:
\[A = \int\limits_{ - 1}^4 \sqrt {3x + 4} dx\] ……………..(1)
Put \[3x + 4 = {t^2}\] ………..(2)
Then, differentiating both sides of the above equation and we get
\[3dx = 2tdt\]
\[ \Rightarrow dx = \dfrac{2}{3}tdt\] <sub>……..(3)

Substitute (2) and (3) in equation (1), we get</sub>
\[A = \int\limits_{ - 1}^4 t \dfrac{2}{3}\, \times tdt\]
_{Integrating and we get}
\[A = \left( {\dfrac{2}{3}} \right)\left[ {\dfrac{{{t^3}}}{3}} \right]_{ - 1}^4\]
\[ = \left( {\dfrac{2}{9}} \right)\left[ {64 + 1} \right]\]
\[ = \left( {\dfrac{2}{9}} \right) \times 65\]
\[ = \dfrac{130}{9}uni{t^2}\]

Similarly, We get B as $\dfrac{130}{9}$,
Therefore,
\[A:B\]=\[\dfrac{130}{9}:\dfrac{130}{9}\]= \[1:1\]
The correct answer is option A.

Note:By performing a definite integral between the two locations, one can determine the area under a curve between two points. Integrate \[y = f\left( x \right)\]between the limits of \[a\] and \[b\]to determine the area under the curve \[y = f\left( x \right)\]between \[x = a\] & \[x = b\]. With the aid of integration and the specified constraints, this area can be easily identified.