Question

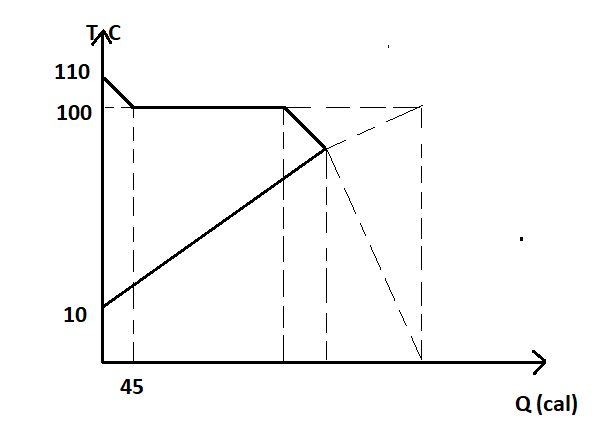
- What is the final equilibrium temperature (approximately) ? This graph is drawn for water. Take the initial amount of water as 21.33 gm.

A) \[{75^\circ }C\]
B) \[{65^\circ }C\]
C) \[{85^\circ }C\]
D) \[{88^\circ }C\]

Answer 1

Hint: The amount of heat supplied or rejected / absorbed is given by \[Q = mS\Delta T\], and in practical situations it is shown by its degree of hotness or coldness. To find the equilibrium temperature we are using this formula, the amount of energy absorbed by water is utilized to raise its temperature and energy rejected by vapour results in conversion of phase and then decrease in temperature, after some time times a point is obtained when there is no transfer of heat take place means the equilibrium position is reached and the temperature obtained here is Equilibrium temperature.

Complete step by step solution:
For water we know that
The specific heat of the steam is (\[{S_v}\])
\[ \Rightarrow {S_v} = 1.5\dfrac{{cal}}{{gm}}\]
The specific heat of water is (\[{S_w}\])
\[ \Rightarrow {S_w} = 1\dfrac{{cal}}{{gm}}\]
The latent heat of water is (\[{L_v}\])
\[ \Rightarrow {L_v} = 540\dfrac{{cal}}{{gm}}\]
The initial amount of water is = 21.33 gm
Let the mass of vapour is \[{m_v}\]
From the graph shown above
\[ \Rightarrow {m_v}{S_v}(110 - 100) = 45cal\]
\[ \Rightarrow {m_v} = \dfrac{{45}}{{{S_v}(110 - 100)}}\]
solving the equation we get with,
\[ \Rightarrow {m_v} = \dfrac{{45}}{{1.5 \times 10}}\]
\[ \Rightarrow {m_v} = 3gm\]\[{L_v} = 540\dfrac{{cal}}{{gm}}\]
Thus, we have determined the mass of the vapour as \[{m_v} = 3gm\].
From the graph at the equilibrium temperature T,
\[ \Rightarrow 45 + {m_v}{L_v} = {m_w}{S_w}(\Delta T)\]
Here \[\Delta T = T - 10\]; and putting the value we get
\[ \Rightarrow 45 + {m_v}{L_v} = {m_w}{S_w}(T - 10)\]
Putting all the values \[{m_v} = 3gm\], \[{S_v} = 1.5\dfrac{{cal}}{{gm}}\] and \[{S_w} = 1\dfrac{{cal}}{{gm}}\], & we get
\[ \Rightarrow 45 + 3 \times 540 = 21.33 \times 1(T - 10)\]
Simplifying the equation we get
\[ \Rightarrow \dfrac{{1665}}{{21.33}} = (T - 10)\]
Solving it for ( T ) we get ,
\[ \Rightarrow 78.05 + 10 = T\]
\[ \Rightarrow T = 88.05^\circ C\]
Hence the equilibrium temperature is \[T = 88.05^\circ C\].

Option (D) is the correct answer.

Note: In fluids at equilibrium position external force is balanced by a pressure-gradient force.
For example: The pressure gradient force prevents gravity from collapsing Earth’s atmosphere into a thin, dense shell, whereas gravity prevents the pressure – gradient force from diffusing the atmosphere into space.