Question

Equation of circle touching and $x=0, y=0$ and $x=4$ is
A) $4\left(x^{2}+y^{2}\right)-16 x-16 y+16=0$
B) $4\left(x^{2}+y^{2}\right)-12 x-12 y+12=0$
C) $4\left(x^{2}+y^{2}\right)-8 x-8 y+4=0$
D) [1] $x^{2}+y^{2}-x-y-1=0$

Answer 1

Hint: To find the equation of the circle we will use the standard form of the equation of a circle. We know that the standard form of equation of a circle is $(x-h)^{2}+(y-k)^{2}=r^{2}$ where $(h,k)$ are the coordinates of the center of the circle, $(x, y)$ are any point on the circle and $r$ is the radius of the circle. We will first draw the diagram of the circle touching line $x=4$ and $x=0,y=0$. With the help of the diagram we will derive the coordinates of the center $(h,k)$ and radius $r$. We will then substitute these values in the standard equation of the circle and then simplify to find the equation of the circle.

Complete step-by-step solution:
The center of a circle is a location inside the circle that is situated in the middle of the circumference.The radius of a circle is the constant distance from the circle's center to any point on the circle.A circle's diameter is defined as the segment of a line that connects two locations on the circle and passes through its center.
We are given a circle which is touching $x=0, y=0$ and $x=4$ and we have to determine its equation. Equation for a circle with a radius of $r$and a center of $(h, k)$ is,
$\Rightarrow(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}$.
We will first draw the diagram of a circle touching $x=0, y=0$ and $x=4$ to determine the radius and center of the circle.

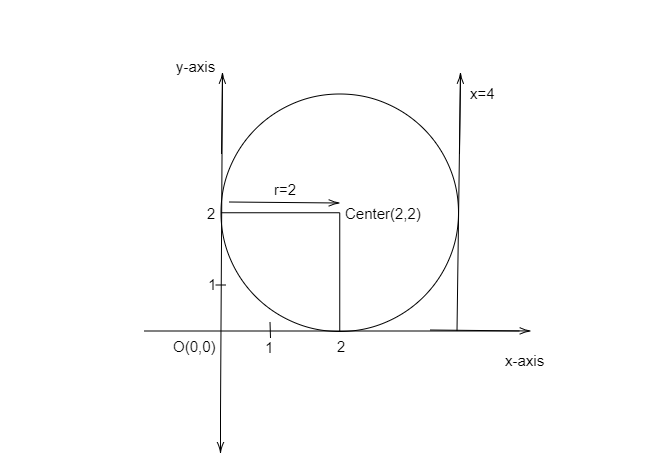
From the diagram we can say that the radius of the circle is $r=2$ and the center is $(2,2)$.
Substituting the values derived,
$\Rightarrow(\mathrm{x}-2)^{2}+(\mathrm{y}-2)^{2}=2^{2}$
Expand the terms inside the brackets
$\Rightarrow \mathrm{x}^{2}-4 \mathrm{x}+4+\mathrm{y}^{2}+4 \mathrm{y}+4=4$
$\Rightarrow \mathrm{x}^{2}+\mathrm{y}^{2}-4 \mathrm{x}-4 \mathrm{y}=-4$
Multiplying throughout by 4 ,
$\Rightarrow 4\left(x^{2}+y^{2}\right)-16 x-16 y+16=0$
So the correct answer is option(A)

Note:
 In the given question the equation of the circle will have only the undefined variables x and y.
And the h and k are the center points. We have to substitute the h and k values to find the equation of the circle. No need to substitute values for x and y.