Question

Ellipse has OB as a semi-minor axis \[F\] and \[F'\] its foci and the angle \[FBF'\] is a right angle. Then what is the eccentricity of an ellipse?
A. \[\dfrac{1}{{\sqrt 3 }}\]\[\]
B. \[\dfrac{1}{4}\]
C. \[\dfrac{1}{2}\]
D. \[\dfrac{1}{{\sqrt 2 }}\]

Answer 1

Hint: We will apply Pythagoras theorem in triangle \[FBF'\] to find the relation between eccentricity (\[e\]), semi minor axis length (\[b\]) and semi major axis length (\[a\]). Then we will use the relation between \[e\], \[b\] and \[a\].

Formula used: \[{e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}\]
Where,
\[e\] is eccentricity of the ellipse
\[b\] is length of minor axis of the ellipse
\[a\] is the length of major axis of the ellipse

Complete step by step solution: Let us assume the ellipse to be of standard form having a major axis along x-axis and a minor axis along y-axis and its eccentricity be \[e\].
Then
\[0 = (0,0)\]
\[F = (ae,0)\]
\[F' = ( - ae,0)\]
\[B = (0,b)\]


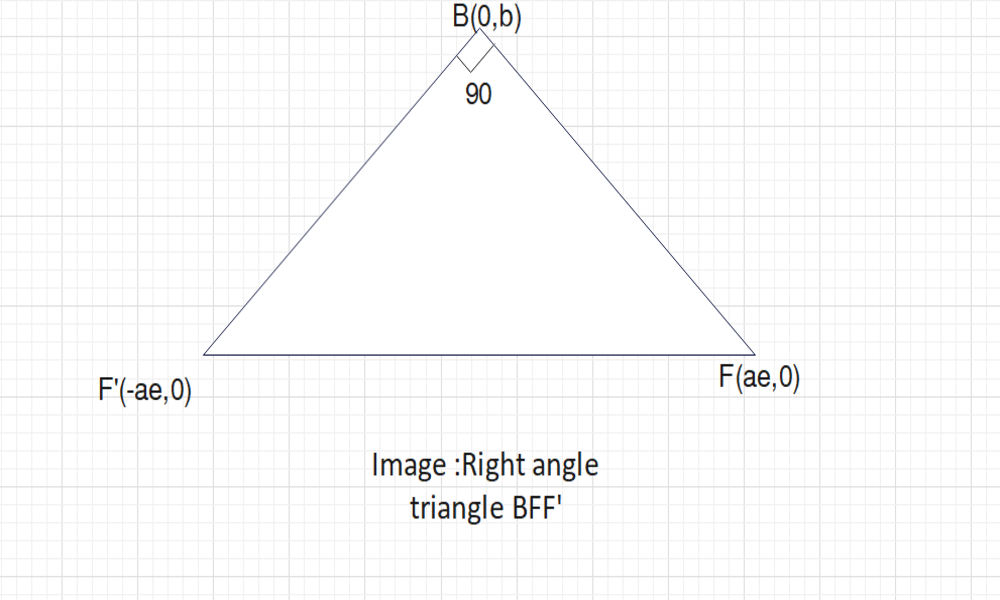
Using the Pythagoras theorem in triangle \[FBF'\]-
\[B{F^2} + BF{'^{\,2}} = FF{'^{\,2}}\] …(1.1)
We know that the distance between two points \[{P_1}({x_1},{y_1})\] and \[{P_2}({x_2},{y_2})\] can be calculated by distance formula as –
\[{P_1}\,{P_2} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} \]
Thus –
\[BF = \sqrt {{{\left( {0 - ae} \right)}^2} + {{\left( {b - 0} \right)}^2}} \]
\[ \Rightarrow BF = \sqrt {{{\left( {ae} \right)}^2} + {{\left( b \right)}^2}} \]
\[BF' = \sqrt {{{\left( {0 - ( - ae)} \right)}^2} + {{\left( {b - 0} \right)}^2}} \]
\[FF' = \sqrt {{{\left( {ae - ( - ae)} \right)}^2} + {{\left( {0 - 0} \right)}^2}} \]
Also
\[FF' = \sqrt {{{\left( {ae - ( - ae)} \right)}^2} + {{\left( {0 - 0} \right)}^2}} \]
\[ \Rightarrow FF' = \sqrt {{{\left( {2ae} \right)}^2}} \]
 Putting the above values in equation (1.1)
\[{\left( {\sqrt {{{\left( {ae} \right)}^2} + {b^2}} } \right)^2} + {\left( {\sqrt {{{\left( {ae} \right)}^2} + {b^2}} } \right)^2} = {\left( {2ae} \right)^2}\]
Solving the above equation
\[2{\left( {\sqrt {{{\left( {ae} \right)}^2} + {b^2}} } \right)^2} = 4{a^2}{e^2}\]
\[ \Rightarrow {\left( {\sqrt {{{\left( {ae} \right)}^2} + {b^2}} } \right)^2} = 2{a^2}{e^2}\]
\[ \Rightarrow {\left( {ae} \right)^2} + {b^2} = 2{a^2}{e^2}\]
\[ \Rightarrow {b^2} = {a^2}{e^2}\]
On cross multiplying by \[{a^2}\]on both sides
\[{e^2} = \dfrac{{{b^2}}}{{{a^2}}}\] …(1.2)
We know that
\[{e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}\]
\[ \Rightarrow \dfrac{{{b^2}}}{{{a^2}}} = 1 - {e^2}\] …(1.3)
Using the equation (1.2) and (1.3)
\[ \Rightarrow 1 - {e^2} = {e^2}\]
Solving the equation
\[ \Rightarrow \,2{e^2} = 1\]
\[ \Rightarrow {e^2} = \dfrac{1}{2}\]
\[ \Rightarrow e = \dfrac{1}{{\sqrt 2 }}\]

So, Option ‘D’ is correct

Note: 1. The most common doubt a student can get here is which form of an ellipse is to be chosen to proceed to a solution. Since the triangle FBF’ is right angle holds for all ellipses, hence we can choose any of them ellipses. Hence, we have chosen the most standard form of the ellipse to ease the calculation.
2. A rough diagram must be drawn in such situations for better understanding.