




Difference Between Parallel and Consecutive Reactions with Examples
The study of Parallel First Order Reaction Kinetics is vital for understanding mechanisms where a single reactant transforms into two or more products via competing pathways, each following first order kinetics. Mastering this concept helps JEE Main aspirants tackle questions on reaction mechanisms, rate laws, and product distributions, making it a high-yield topic for exam success in physical chemistry.
What is a Parallel First Order Reaction?
A parallel first order reaction occurs when a reactant (A) undergoes two or more simultaneous transformations to yield different products (B, C, etc.), each through its own pathway and rate constant. For example, A can decompose to form B via rate constant k1 and independently form C via k2, both simultaneously.
A real-world analogy is choosing different exits in a metro station—one passenger can independently choose any exit at any time; each exit represents a reaction pathway and the total number leaving is split among them.
Such reactions are common in organic chemistry, like the hydrolysis of esters or the decomposition of substituted alkyl halides, where a molecule can react with more than one reagent or via multiple mechanisms at once.
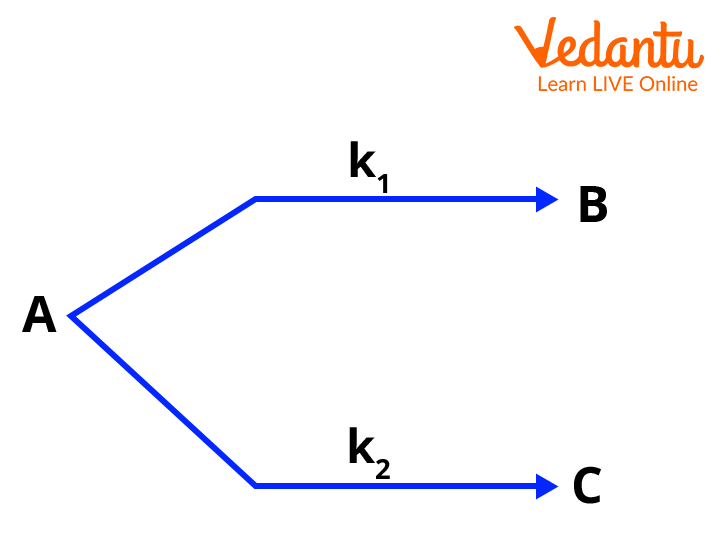
Parallel vs Consecutive Reactions: Key Differences
Parallel reactions (side reactions) involve a single reactant forming multiple products at the same time, while consecutive reactions involve products being formed in a sequence (product of one step becomes reactant for the next).
| Feature | Parallel First Order | Consecutive First Order |
|---|---|---|
| Pathway | Reactant splits into multiple products simultaneously | Products formed in a specific order, stepwise |
| Rate law | Sum of first order rate constants | Depends on intermediate formation and decay |
| Graph | [A] decreases, [B] and [C] rise together | [A] falls, [B] rises then falls, [C] rises |
| Example | Nitration of phenol (ortho- and para- products) | Hydrolysis of ester (via intermediate acid or alcohol) |
For JEE Main, distinguishing these types is crucial for reaction mechanism MCQs and when choosing correct rate laws.
Kinetics and Rate Law Derivation for Parallel First Order Reactions
Consider the system: A → B (rate constant k1), A → C (rate constant k2). Both reactions follow first order kinetics with initial concentration a for A.
- Rate of formation of B: d[B]/dt = k1[A]
- Rate of formation of C: d[C]/dt = k2[A]
- Overall rate of disappearance of A: d[A]/dt = -(k1 + k2)[A]
Integrating, we get the combined rate law for parallel first order reaction kinetics:
- [A] = a × exp[-(k1 + k2)t]
- ktotal = k1 + k2
- [B] = (a × k1 / (k1 + k2)) × [1 - exp(−(k1 + k2)t)]
- [C] = (a × k2 / (k1 + k2)) × [1 - exp(−(k1 + k2)t)]
The fraction of B vs C formed depends directly on the ratio k1 : k2. If asked for product distribution, use these ratios for quick calculations.
A key point: if both pathways have equal rate constants, products will form in a 1:1 ratio. Applying these formulas correctly can instantly solve many JEE chemistry numericals.
Graphical Representation of Parallel First Order Kinetics
The concentration vs. time plot for parallel first order reactions shows exponential decay of [A] and simultaneous exponential growth for [B] and [C], reaching a combined maximum equal to initial a as t → ∞.
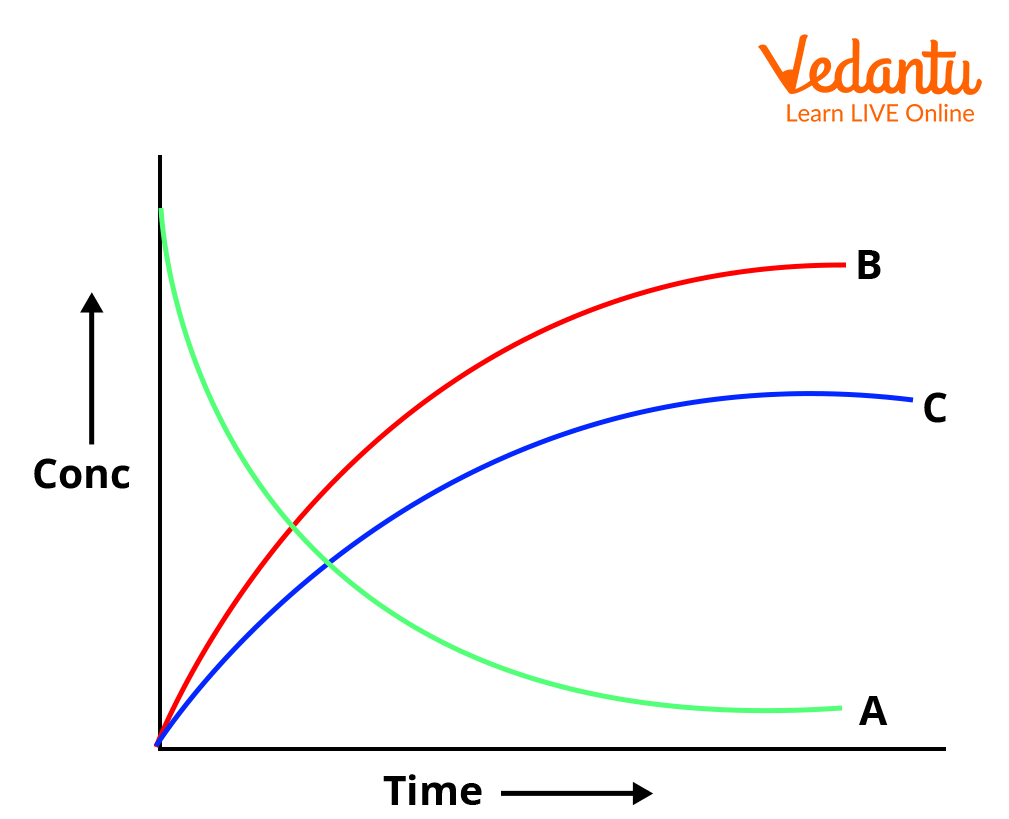
Always remember to compare with consecutive reactions: intermediates in series show maxima, but parallel products increase monotonically with time.
Examples and JEE-Style Applications of Parallel First Order Reaction Kinetics
A classic parallel reaction example is the hydrolysis of tert-butyl chloride in aqueous ethanol:
- (CH3)3CCl + H2O → (CH3)3COH + HCl (k1)
- (CH3)3CCl + C2H5OH → (CH3)3COC2H5 + HCl (k2)
Here, both water and ethanol compete for the same reactant, producing different products in parallel.
- JEE Question: If k1 = 0.01 min-1 and k2 = 0.02 min-1, what fraction of (CH3)3COH forms as t → ∞?
Solution: Fraction for alcohol = k1/(k1 + k2) = 0.01/0.03 = 0.33 or 33%. The remaining 67% is ether.
- In organic synthesis, controlling conditions (temperature, solvent) can alter the value of k1 and k2, helping chemists maximize the desired product.
- Industrially, parallel first order kinetics helps predict product distribution in bulk organic reactions or pharmaceutical intermediates.
Summary Notes: Parallel First Order Reaction Kinetics
- Single reactant forms multiple products at same time, each by first order law.
- Overall rate constant is sum: ktotal = k1 + k2 + …
- [A] decreases exponentially; product amounts depend on k1:k2 ratios.
- Parallel mechanisms differ from consecutive (series) reactions in pathway and product profiles.
- Apply: Use to solve product distribution, rate law, and concentration vs. time problems in JEE Main physical chemistry.
Further Reading and Related JEE Chemistry Topics
- Chemical Kinetics – Concepts, Units and Formulas
- First Order Reaction – Rate Law, Formula, and Examples
- Rate Law and Its Types
- Factors Affecting Rate of Reaction
- Law of Mass Action and Its Applications
Content reviewed by Vedantu’s Chemistry team for JEE. For downloadable notes and practice problems on parallel first order reaction kinetics, visit Vedantu’s online study resources.
FAQs on Parallel First Order Reaction Kinetics Explained
1. What is a parallel first order reaction?
Parallel first order reaction kinetics involve a single reactant converting into two or more products simultaneously via different pathways, each following first order kinetics.
Key points include:
- All reaction branches start from the same reactant.
- Each pathway has its own first order rate constant (such as k1, k2).
- The overall decay rate is the sum of the individual parallel rates.
2. What is the difference between parallel and consecutive reactions?
Parallel reactions and consecutive reactions differ in how the reactants and products are connected:
- Parallel reactions: One reactant forms different products at the same time via independent pathways.
- Consecutive reactions: One product of the first step becomes the reactant for the next step (stepwise sequence).
- Parallel: A → B and A → C at the same time.
- Consecutive: A → B → C in steps.
3. What is the rate law for parallel first order reactions?
The rate law for a parallel first order reaction states that the overall disappearance of the reactant is the sum of the individual parallel rates.
Rate = -(d[A]/dt) = (k1 + k2 + ... ) [A]
Highlights:
- k1, k2, etc., are rate constants for each pathway.
- This means the reactant decays faster compared to just a single pathway.
- The combined rate constant is often written as ktotal = k1 + k2 + ...
4. Can you provide an example of a parallel reaction?
A classic example of a parallel first order reaction is the decomposition of hydrogen peroxide (H2O2) which can decompose via two pathways:
- H2O2 → H2O + ½ O2 (pathway 1)
- H2O2 → H2O + O (pathway 2)
5. Why are parallel reactions important in reaction kinetics?
Parallel reactions are important because they:
- Help predict product distribution when a reactant can form several products.
- Allow calculation of yield and rate for each product branch.
- Model real chemical and biological systems (e.g., drug metabolism, complex syntheses).
6. What is meant by double first order in parallel reactions?
Double first order in parallel reactions means the reactant undergoes two simultaneous first order processes through separate pathways.
- Both pathways follow first order kinetics, each with its own rate constant (k1, k2).
- The total rate constant is the sum: ktotal = k1 + k2.
7. How do you identify parallel reactions in JEE or NEET exam numericals?
To quickly identify parallel reactions in exam questions:
- Look for a single reactant giving two or more products at the same time.
- The question will mention independent reaction paths, usually with separate rate constants.
- Schematic representation usually shows one reactant branching to multiple products.
8. Can a reaction be both parallel and consecutive at once?
Yes, some complex reaction mechanisms may have both parallel and consecutive steps.
- These often involve an initial reactant splitting into several pathways (parallel) and then those products further reacting in sequence (consecutive).
- Such mixed mechanisms require combined kinetic approaches and careful analysis in advanced problems or research settings.
9. Is the half-life calculation different for parallel reactions?
For parallel first order reactions, the half-life (t1/2) is determined by the sum of the rate constants:
- t1/2 = 0.693 / (k1 + k2 + ...)
10. What happens if the rate constants for the parallel paths are equal?
If parallel rate constants are equal (k1 = k2):
- Each product is formed at the same rate from the reactant.
- The overall decay rate doubles (ktotal = 2k for two paths).
- Product ratio remains 1:1, making calculation and prediction simpler in exam questions.























