Question

Assertion
Two vectors are said to be like vectors if they have the same direction but different magnitude.
Reason
vector quantity does not have a specific direction
A) Both assertion and reason are correct and the reason is the correct clarification for the assertion.
B) Both assertion and reason are correct and the reason isn't the right clarification for the assertion.
C) Assertion is correct however the reason is wrong.
D) Both assertion and reason are wrong.

Answer 1

Hint:
In this question, we have been asked about the like vectors and the vector's quantity. Therefore, from the definition of the like vectors and the vector quantity, we will get the result. Hence, we will select a suitable answer.


Complete step by step solution:
Now we know that if two vectors are in the same direction, then those vectors are known as like vectors. And if the two vectors are not in the same direction, then those vectors are known as, unlike vectors.
Suppose that there are two vectors \[\overrightarrow A \]and \[\overrightarrow B \]respectively. And both the vectors are in the same direction as shown in the figure.

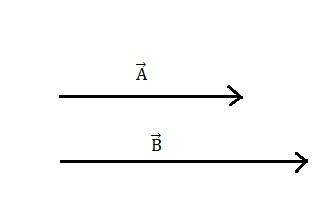
Figure 1
 Then these vectors are said to be like vectors.
Vector quantity is a physical quantity which has both direction and magnitude. It means that If any physical quantity has a direction, then that quantity will be a vector quantity. Vector quantity has a particular direction.
From the above explanation, we can conclude that the assertion is right and the reason is wrong.
Therefore, the correct option is C.




Note:
In this question, it is important to note that the vectors that have the same direction, are called the like vectors. If the magnitude of these vectors is different, then these vectors are also said to be like vectors.