Question

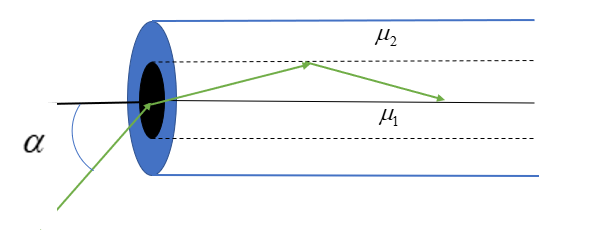
An optical fiber consists of core of ${\mu _1}$​ surrounded by a cladding of ${\mu _2} < {\mu _1}$ A beam of light enters from air at an angle α with axis of fiber. The highest α for which ray can be traveled through fiber is

A. ${\cos ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
B. ${\sin ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
C. ${\sec ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
D. ${\tan ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $

Answer 1

Hint: In this question we will be using the snell's law and basic trigonometric identities to solve and get the desired answer. When light travels from one medium to another, Snell's law is used to link the angle of incidence and angle of reflection with the refractive index of a medium.


Formula used:

$\dfrac{{\sin \alpha }}{{\sin r}} = {\mu _1}$


Complete step by step solution:
Refraction is the study of how light bends when it comes into contact with two media that have different refractive indices. As a result, the refractive indices of the two media may be related through the angle associated with incidence and refraction.
Snell’s law: The reciprocal of the ratio of the indices of refraction, or the ratio of phase velocities in the two media, is said to be identical to the ratio of the sines of the angles of incidence and refraction.
$\dfrac{{\sin \alpha }}{{\sin r}} = {\mu _1}$ --------- (1)
Where ${\mu _1} = $refractive index of medium 1,
$\alpha$ is angle of incident
$r$ is the angle of refraction
So that TIR take place at core and cladding interface
$90 - {\theta _c} > r$ where $\sin {\theta _c} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
$ \Rightarrow \sin (90 - {\theta _c}) > \sin r$ ------ (2)
Also using equation 1 we get
$\sin \alpha = {\mu _1}\sin r$ ---------(3)
So, from equation 2 and 3 we get
$\cos {\theta _c} > \dfrac{{\sin \alpha }}{{{\mu _1}}}$
Also, we know that $\cos {\theta _c} = \sqrt {1 - {{\sin }^2}{\theta _c}} $
From 1st equation $\cos {\theta _c} = \sqrt {1 - \dfrac{{{\mu ^2}_2}}{{{\mu ^2}_1}}} $
$ \Rightarrow \sin \alpha < {\mu _1}\sqrt {1 - \dfrac{{{\mu ^2}_2}}{{{\mu ^2}_1}}} $
\[ \Rightarrow \sin \alpha < \sqrt {{\mu ^2}_1 - {\mu ^2}_2} \]
$\therefore {\alpha _{\max }} = {\sin ^{ - 1}}\sqrt {{\mu ^2}_1 - {\mu ^2}_2} $
Hence option B is correct.



Note: Refraction only occurs when light rays go from a denser to a less common medium. This is due to the fact that total internal refraction cannot occur when light rays move from a rarer to a denser medium since the refracted angle is always smaller than the incident angle. Since the angle of incidence can never be more than 90 degrees, neither can the angle of refraction.