Question

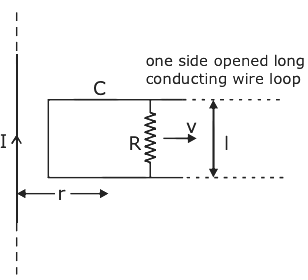
An infinitely long straight wire carrying current I, one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane, as shown in the figure. The connector has length l and resistance R. It slides to the right with a velocity v. The resistance of the conductor and the self-inductance of the loop are negligible. The induced current in the loop, as a function of separation r, between the connector and the straight wire is:
1) $\dfrac {\mu_0}{2\pi} ~\dfrac {Ivl}{Rr}$
2)$\dfrac {\mu_0}{\pi} ~\dfrac {Ivl}{Rr}$
3) $\dfrac {2 {\mu_0}}{\pi} ~\dfrac {Ivl}{Rr}$
4) $\dfrac {\mu_0}{4 \pi} ~\dfrac {Ivl}{Rr}$

Answer 1

Hint: Firstly, we should know about resistance of the conductor. The inherent resistance to current flow in a conductor is known as conductor resistance. Less resistance to current flow is provided by materials the more electrically conductive they are. Less conductivity results from increased conductor resistance to current flow..

Complete answer:
A conductor experiences resistance as a result of free electrons. These unimpeded electrons crash with one another as well as with the ions and atoms that stand in their way. Resistance is the term for this hindrance.

Resistance is influenced by the following variables:
$\bullet$ The conductor's length
$\bullet$ Cross-sectional area
$\bullet$ The building's composition

At a temperature of 20°C, one can determine a conductor's resistance by using:
$Resistance = Resistivity \times \dfrac {Length} {Area}$
$R=\rho *(L/A)$
where:
R is the resistance, expressed in ohms.
ρ is the material's resistivity expressed in ohm metres (m)
L is the conductor's length in metres (m)
A is the conductor's cross-sectional area in square metres ($m^2$)

We start by stating the apparent truth that a conductor's length affects its overall resistance. Generally speaking, a conductor will have more resistance the longer it is. This is seen in the relationship described above.

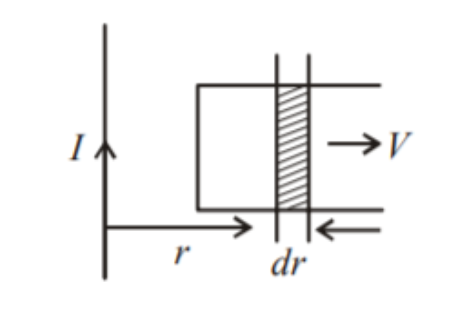
Now, the Magnetic field at a distance r from the wire. Magnetic flux for small displacement $dr$,
$\phi =B.A=Bldr$
$\because A=ldr$ and $B.A=BA\cos {{0}^{0}}$
$\Rightarrow \phi =\dfrac{{{\mu }_{0}}I}{2\pi r}ldr$


Emf,
$e=\dfrac{d\phi }{dt}=\dfrac{{{\mu }_{0}}Il}{2\pi r}.\dfrac{dr}{dt}$
$\Rightarrow e=\dfrac{{{\mu }_{0}}}{2\pi }.\dfrac{Ivl}{r}$

Induce current in the loop,
$i=\dfrac{e}{R}$
$i=\dfrac{{{\mu }_{0}}}{2\pi }.\dfrac{Ivl}{Rr}$

Therefore, option (1) is correct.

Note: The cross-sectional area of the chosen conductor is a crucial component in determining conductor resistance. It's significant to remember that a conductor's resistance and cross-sectional area are inversely correlated. The conductor's resistance value increases as the conductor's cross-sectional area decrease. This indicates that there is a trade-off between resistance and cost when using smaller conductor diameters.