Question

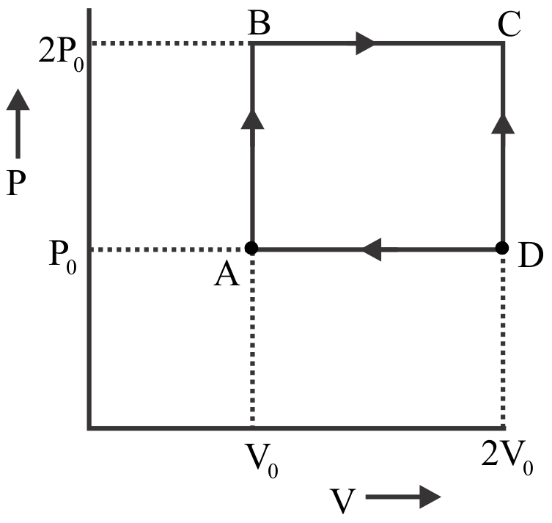
An engine operates by taking n moles of an ideal gas through the cycle ABCDA shown in the figure. The thermal efficiency of the engine is: (Take${C_v} = 1.5R$, where $R$, is gas constant)

$\left( a \right)$ $0.32$
$\left( b \right)$ $0.24$
$\left( c \right)$ $0.15$
$\left( d \right)$ $0.08$

Answer 1

Hint Since we have to find thermal efficiency. So for this, first of all, we know the work done will be $W = {P_0}{V_0}$and also from the ABCDA we can say that the heat given will be equal to the sum of heat produced by $Q$ through $AB$and heat produced by $Q$ through$BC$. And by using the heat formula we can solve this problem.
Formula used:
Work is done,
$W = {P_0}{V_0}$
Here,
${P_0}$, will be the pressure
${V_0}$, will be the volume
Heat given will be equal to,
$ \Rightarrow n{c_v}dt + n{c_p}dt$
Here,
$dt$, will be the change in the temperature
${c_p}and{\text{ }}{{\text{c}}_v}$, will be the pressure and the volume respectively.

Complete Step By Step Solution
As we know the formula of work done which is equal to the
$W = {P_0}{V_0}$
So from the question, we can write the heat given
Heat given will be equal to,
Heat has given $ = {Q_{AB}} + {Q_{BC}}$
Now by using the heat given formula mentioned above, we can write it as
$ \Rightarrow n{c_v}d{t_{AB}} + n{c_p}d{t_{BC}}$
As we already know the value of ${C_v} = 1.5R$
Therefore substituting this value in the heat given equation, we get
Heat gave $ = \dfrac{3}{2}\left( {nR{T_B} - nR{T_A}} \right) + \dfrac{5}{2}\left( {nR{T_C} - nR{T_B}} \right)$
For the monatomic gas, the value will be 3
Now putting the values we had calculated above, we get
$ \Rightarrow \dfrac{3}{2}\left( {2{P_0}{V_0} - {P_0}{V_0}} \right) + \dfrac{5}{2}\left( {4{P_0}{V_0} - 2{P_0}{V_0}} \right)$
On simplifying the solution, we get
$ \Rightarrow \dfrac{{13}}{2}{P_0}{V_0}$
As we know the formula for efficiency can be given by
$\eta = \dfrac{W}{{heat{\text{ gain}}}}$
It can also be written in the following way and also substituting the values, we get
$ \Rightarrow \dfrac{{{P_0}{V_0}}}{{\dfrac{{\dfrac{{13}}{2}}}{{{P_0}{V_0}}}}}$
On solving,
$ \Rightarrow \dfrac{2}{{13}}$
$ \Rightarrow \eta = 0.15$

Therefore, the option $C$ will be the correct one.

Note Efficiency can be calculated as a function of many parameters, one of which being temperature or the amount of heat supplied.
Thermal efficiency, therefore, is a measure of how well the machine or device has utilized the energy given to it. The term thermal is used simply for the fact that it is related to the temperature parameter. Efficiencies are also calculated in terms of mechanical advantage obtained called the mechanical efficiency