Question

An electric dipole of the moment \[\overrightarrow P \] is placed at the origin along the x-axis. The angle made by the electric field with the x-axis at a point P, whose position vector makes an angle \[\theta \] with the x-axis, is (where \[\tan \alpha = \dfrac{1}{2}\tan \theta \])
A. \[\alpha \]
B. \[\theta \]
C. \[\theta + \alpha \]
D. \[\theta + 2\alpha \]

Answer 1

Hint: If we have two charges, one is positive and one is negative then, the electric dipole gives the direction of the flow of charges. That is, from negative charge toward positive charge. The electric field intensity is defined as a force experienced by a unit positive charge placed at some point in the electric field.

Formula Used:
To find the electric field the formula is,
\[E = \dfrac{P}{{4\pi {\varepsilon _0}}}\dfrac{1}{{{r^3}}}\sqrt {3{{\cos }^2}\theta + 1} \]
Where, P is electric dipole moment and r is distance between the two charges.


Complete step by step solution:

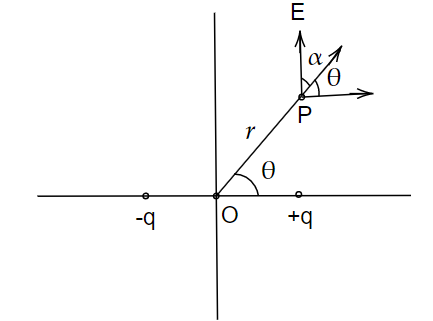
Image: An electric dipole moment placed at the origin along the x-axis.


Consider an electric dipole moment P​ which is placed at the origin along the x-axis. The angle made by the electric field with the x-axis at a point P, then we need to find the electric field.
For that we consider the diagram where the dipole is placed on the x-axis, now we have to find the electric field at point P. The position vector makes an angle \[\theta \] with the x-axis denoted by \[\overrightarrow r \] from point P to the dipole. Then the formula to find the electric field is given by,
\[E = \dfrac{P}{{4\pi {\varepsilon _0}}}\dfrac{1}{{{r^3}}}\sqrt {3{{\cos }^2}\theta + 1} \]

Further, we know that the electric field at the point P makes an angle\[\alpha \]with respect to the position vector and the angle \[\theta \] with respect to the x-axis. By this, we can say that the electric field at point P makes an angle of \[\alpha + \theta \] from the x-axis. Therefore, the position vector makes an angle \[\theta \] with x-axis is, \[\alpha + \theta \].

Hence, option C is the correct answer.

Note: Don’t get confused with the terms electric dipole and the dipole moment. When two opposite charges are kept at a certain distance from each other then the system is termed an electric dipole. The dipole moment is always a vector quantity with the direction being from the negative to the positive charge.