Question

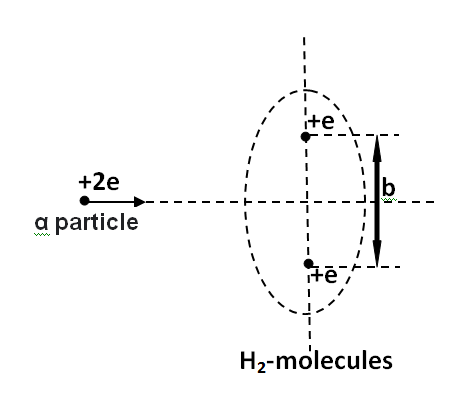
An \[\alpha \] particle passes rapidly through the exact centre of a hydrogen molecule, moving on a line perpendicular to the internuclear axis. The distance between the nuclei is \[b\] . Where on its path does the \[\alpha \] -particle experience the greatest force? Assume that the nuclei do not move much during the passage of the \[\alpha \] particle. Also neglect the electric field of the electrons in the molecule.

A. $\dfrac{b}{2}$
B. $\dfrac{b}{{2\sqrt 2 }}$
C. $\dfrac{b}{{\sqrt 2 }}$
D. None of these

Answer 1

Hint: To solve this question, we will first consider a point on the perpendicular bisector of the line joining the two hydrogen atoms. To find the force between the \[\alpha \] particle and the hydrogen atom, we will consider the \[\alpha \] particle at that point and write the expression of force. Now, we know that the condition to find the extreme value of a function whose first derivative is kept equal to zero. We will use this concept to get the value of the greatest force experienced by the \[\alpha \] particle.

Formula Used:
Force between two charges,
$F = k\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
where ${q_1}\,\& \,{q_2}$ are the two charges and $r$ is the distance between them.
Also, $k = \dfrac{1}{{4\pi { \in _o}}}$
Quotient formula of differentiation,
$\dfrac{d}{{dx}}\left( {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}} \right) = \dfrac{{f'\left( x \right)g\left( x \right) - f\left( x \right)g'\left( x \right)}}{{{{\left( {g\left( x \right)} \right)}^2}}}$

Complete step by step solution:
Given: Charge on a hydrogen atom, ${q_1} = e$
Charge on the \[\alpha \] particles, ${q_2} = 2e$
Distance between the nuclei \[ = b\]

Let $F$ be the force between the \[\alpha \] particle and the hydrogen atom. Draw a perpendicular bisector of the line joining the nuclei of the two hydrogen atoms. Consider a point $P$ on it at a distance \[x\] from the foot of the perpendicular.


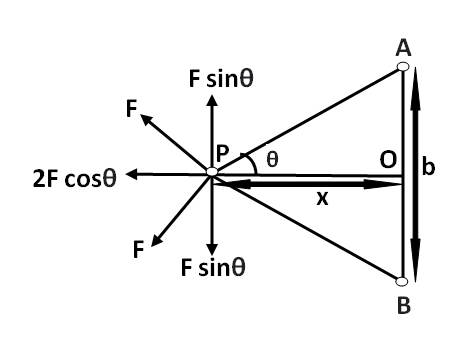
From the diagram above we can see that the vertical components of the force $F$ cancel each other. Hence, the net force becomes,
${F_{net}} = 2F\cos \theta $
Where $\cos \theta = \dfrac{x}{{{{\left( {{x^2} + {{\left( {\dfrac{b}{2}} \right)}^2}} \right)}^{\dfrac{1}{2}}}}}$
(denominator is obtained using Pythagoras theorem in $\vartriangle AOP$ )
This implies,
\[{F_{net}} = 2F\dfrac{x}{{{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}}}}\] ...(1)

Also,
$F = k\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
That is,
$F = k\dfrac{{\left( e \right)\left( {2e} \right)}}{{{{\left( {{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}}} \right)}^2}}} \\ $...(2)
Substituting equation (2) in equation (1), we get,
\[{F_{net}} = 2\left( {k\dfrac{{\left( e \right)\left( {2e} \right)}}{{{{\left( {{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}}} \right)}^2}}}} \right)\dfrac{x}{{{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}}}} \\ \]
Simplifying this, we get,
\[{F_{net}} = \dfrac{{4kx{e^2}}}{{{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{3}{2}}}}}\]

Now, we know that the condition of extremum is: $\dfrac{{d{F_{net}}}}{{dx}} = 0$ , that is, the first derivative is kept equal to zero to find the extreme value of a function.
Using quotient formula we get,
$\dfrac{{d{F_{net}}}}{{dx}} = 4k{e^2}\dfrac{{\left( {1 \times {{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{3}{2}}} - \left( {x \times \dfrac{3}{2}{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}} \times 2x} \right)} \right)}}{{{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^3}}} \\ $
Putting this equal to zero, we get,
 $4k{e^2}\dfrac{{\left( {1 \times {{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{3}{2}}} - \left( {x \times \dfrac{3}{2}{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}} \times 2x} \right)} \right)}}{{{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^3}}} = 0$

Simplifying this, we get,
$\left( {1 \times {{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{3}{2}}} - \left( {x \times \dfrac{3}{2}{{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)}^{\dfrac{1}{2}}} \times 2x} \right)} \right) = 0 \\ $
This implies,
$\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right){\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)^{\dfrac{1}{2}}} = 3{x^2}{\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right)^{\dfrac{1}{2}}} \\ $
Solving this, we get,
$\left( {{x^2} + \dfrac{{{b^2}}}{4}} \right) = 3{x^2} \\ $
This gives, $2{x^2} = \dfrac{{{b^2}}}{4} \\ $
Hence, $x = \pm \dfrac{b}{{2\sqrt 2 }}$
Thus, the $\alpha $ particle experience greatest force at a distance $x = \pm \dfrac{b}{{2\sqrt 2 }}$ from the foot of the perpendicular bisector of the line joining the nuclei of the two hydrogen atoms.

Hence, option B is the correct answer.

Note: Before doing this question one must know the rules of differentiation. Also, an important point to note in this question is that the direct expression of force between the $\alpha $ particle and a hydrogen atom is not the net force. We need to take into consideration the components of this force.