Question

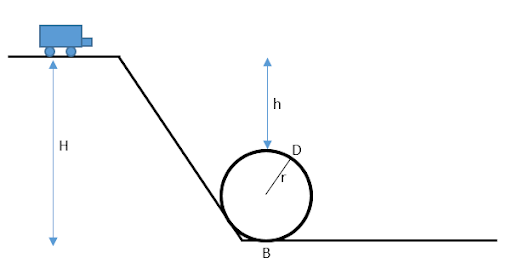
A toy car rolls down the inclined plane as shown in the above figure. It loops at the bottom. What is the relation between H and h?

A. \[\dfrac{H}{h} = 2\]
B. \[\dfrac{H}{h} = 3\]
C. \[\dfrac{H}{h} = 4\]
D. \[\dfrac{H}{h} = 5\]

Answer 1

Hint:When the path of the motion is frictionless then we use conservation of mechanical energy. To loop throughout the minimum velocity at the top of the loop be such that the produced centrifugal force balances the weight of the body.

Formula used:
\[K = \dfrac{{m{v^2}}}{2}\]
Here K is the kinetic energy of mass m moving with velocity v.
\[U = mgh\]
Here U is the gravitational potential energy of mass m at height h and g is the acceleration due to gravity.

Complete step by step solution:
The initial velocity of the car at height H is 0 m/s as it is at rest. Let the velocity of the car at the lowest point of the loop is \[v\]. Then using the conservation of mechanical energy of the car, the total energy of the car at height H will be conserved and will be equal to the mechanical energy of the car at the lowest point of the loop.

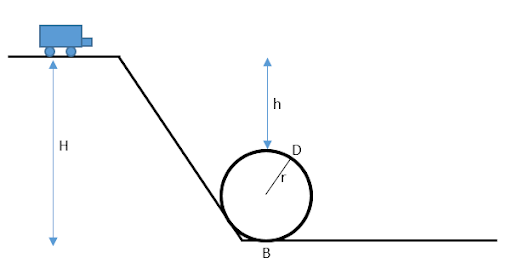
Image: The toy car rolls down

\[{E_{top}} = {E_{bottom}}\]
\[\Rightarrow {\left( {U + K} \right)_{top}} = {\left( {U + K} \right)_{bottom}}\]
\[\Rightarrow mgH + \dfrac{{m \times {{\left( 0 \right)}^2}}}{2} = mg \times \left( 0 \right) + \dfrac{{m \times {v^2}}}{2}\]
\[\Rightarrow v = \sqrt {2gH} \ldots \left( i \right)\]
As we know that to complete the loop the minimum velocity needed at the lowest point of the loop is equal to \[\sqrt {5gr} \]
So,
\[v = \sqrt {5gr} \ldots \left( {ii} \right)\]

From both the equations, we get
\[\sqrt {2gH} = \sqrt {5gr} \Rightarrow H = \dfrac{{5r}}{2} \ldots \left( {iii} \right)\]
From the shown figure,
\[H = h + 2r\]
Substituting 3rd equation, we get
\[h = \dfrac{{5r}}{2} - 2r \\
\Rightarrow h = \dfrac{r}{2} \ldots \ldots \left( {iv} \right)\]
From 3rd and 4th equations,
\[\dfrac{H}{h} = \dfrac{{\left( {\dfrac{{5r}}{2}} \right)}}{{\left( {\dfrac{r}{2}} \right)}} = 5\]
\[\therefore \dfrac{H}{h} = 5\]

Therefore, the correct option is D.

Note: We should be careful about the nature of the path of motion. If the path is frictional then the mechanical energy is lost as work done by the friction. The total mechanical energy of a system is conserved in accordance with the principle of mechanical energy conservation, which states that energy cannot be created or destroyed and can only be internally transformed from one form to another if the forces acting on the system are conservative in nature.