Question

A thin tube sealed at both ends is 100cm long. It lies horizontally, the middle 20cm containing mercury and to ends containing air at standard atmospheric pressure. If the tube is now turned to the vertical position, by what amount will the mercury be displaced?

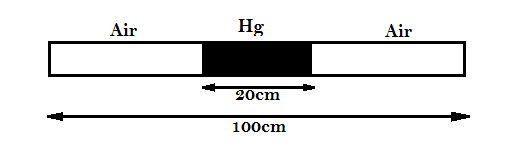
(Given: Cross-section of the tube can be assumed uniform.)
A) 2.95cm
B) 5.18cm
C) 8.65cm
D) 0.0cm

Answer 1

Hint: When the tube is turned to the vertical position, the mercury will shift downwards because of gravity. The air which will be below the mercury will be compressed because of the pressure exerted by the mercury. But the volume of the gas above the mercury will increase. The mass of the gas will remain the same because the number of molecules of the gas will be the same. Therefore use the relation among volume, gas, and pressure to the above question.

Complete step by step solution:
Step 1: Standard atmospheric pressure is usually taken to be 0.760m of Hg at 0°C. When we convert it into the centimeter the pressure will be 76.0cm of Hg. This is the pressure of air when the tube is kept horizontally. Since the molecules of the air are not decreasing or increasing. It is the volume and pressure that are increasing or decreasing. Therefore when the mass of the gas is kept constant then, the relation between pressure and volume is given by ${P_1}{V_1} = {P_2}{V_2}$ , where ${P_1}$ and ${V_1}$ are the pressure and volume respectively when the tube is horizontal, and ${P_2}$ ${V_2}$ are the pressure and volume when the tube is vertical. We are given that ${P_1} = 76.0cm$ of $Hg$ and ${V_1} = 45 \times A$ where $A$ is the cross-section area of the tube and the length of the part in which gas is filled will be 45cm as the length of the tube is 100cm and Hg is filled in 20cm in the middle. When the tube is kept vertical the volume of the gas will change- the volume of the gas above Hg will increase and the volume of the gas below the Hg will decrease. we consider the gas above the Hg. Let Hg shift $x$ distance downward then the volume of the gas will be $\Rightarrow {V_2} = (45 + x)A$ and let the pressure is $P'$ . Therefore,
$\therefore 76.0 \times 45 \times A = P' \times (45 + x)A$
$A$ will be canceled out from both sides
$ \Rightarrow P' = \dfrac{{76 \times 45}}{{45 + x}}$………equation (1).
Step 2: Now consider the changes in the gas below the Hg. The volume will decrease and pressure will increase when the tube is kept vertical. Let the pressure of the gas in the vertical position be $P$ and the volume of the gas will be $(45 - x)A$ , therefore,
$\therefore 76.0 \times 45 \times A = P \times (45 - x)A$
Again $A$ will be canceled out from both sides
$ \Rightarrow P = \dfrac{{76 \times 45}}{{45 - x}}$…..equation (2).
Step 3: Now we have the value of P and P’. since the pressure and volume are equilibrium, therefore the pressure $P$ will be equal to $P' + 20$ . because the pressure of the 20cm mercury is 20cmHg. Therefore we can write
$\therefore P = P' + 20$
From equation (1) and (2)
$\therefore \dfrac{{76 \times 45}}{{45 - x}} = \dfrac{{76 \times 45}}{{45 + x}} + 20$
$ \Rightarrow \dfrac{{76 \times 45}}{{45 - x}} - \dfrac{{76 \times 45}}{{45 + x}} = 20$
$ \Rightarrow 76 \times 45\left( {\dfrac{1}{{45 - x}} - \dfrac{1}{{45 + x}}} \right) = 20$
Subtract the bracket term
$ \Rightarrow 76 \times 45\left( {\dfrac{{45 + x - 45 + x}}{{45 - x}}} \right) = 20$
$ \Rightarrow 76 \times 45\left( {\dfrac{{2x}}{{{{45}^2} - {x^2}}}} \right) = 20$
$ \Rightarrow 342x = {45^2} - {x^2}$
$ \Rightarrow {x^2} + 342x - 2025 = 0$
On solving the above equation for $x$ we get $x = 5.18cm$.

Hence the option B is correct.

Note: Gases are the only state of matter that can be compressed very tightly or expanded to fill a very large space. On the other hand, mercury is a very heavy metal compared to the air. The pressure is inversely proportional to the volume. When the pressure decreases the volume increases therefore we added 20cm of Hg to the less pressured gas which is above the 20cm of Hg.