
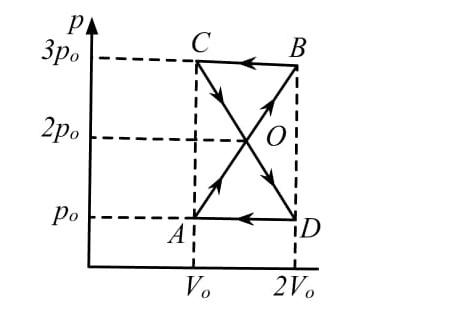
A thermodynamic system undergoes cyclic process ABCDA as shown in the figure. The work done by the system is:
A) ${P_0}{V_0}$
B) $2{P_0}{V_0}$
C) $\dfrac{{{P_0}{V_0}}}{2}$
D) $Zero$
Answer
225.9k+ views
Hint: In order to solve this question, the work done can be calculated by computing the area covered by the pressure-volume graph. The reason is that the work done in a gas is the product of pressure and the volume.
Work done, $W = PV$
Hence, we consider the area under the curve of a P-V graph.
Complete step by step solution:
The work done is defined as the product of the force and the displacement.
$W = Fs$
The pressure is defined as the force per unit area.
$P = \dfrac{F}{A}$
If we consider a gas at a pressure P in a container of cross-section area A, the force exerted is given by –
$F = PA$
Substituting the force in the work done, we get –
$W = PAs$
The product of the area of cross-section of the container of the gas and the distance it travels horizontally, is equal to the volume swept by the gas.
Volume, $V = As$
Hence, the work done is given by –
$W = PV$
Since the work done is the product of pressure and volume, if we plot a graph of pressure and volume of the gas, the area under the curve will be equal to the work done.
If the graph is clockwise, the work is done on the system and its value is positive. If the graph is anti-clockwise, the work done by the system and the value is negative.
Consider a P-V graph as shown:
Work done in the entire process = Area of figure ADOBC
Area of figure ADOBC = Area of triangle AOD + Area of triangle BOC
To calculate the area of triangle AOD, ${A_1}$:
${A_1} = \dfrac{1}{2} \times b \times h$
where b = base of triangle and h = height.
Base, $b = 2{V_0} - {V_0} = {V_0}$
Height, $h = 2{p_0} - {p_0} = {p_0}$
Hence, area of AOD –
$\Rightarrow {A_1} = \dfrac{1}{2} \times {P_0} \times {V_0} = \dfrac{{{P_0}{V_0}}}{2}$
Since the triangle AOD is clockwise, the work done is positive.
$\therefore {W_1} = {A_1} = \dfrac{{{P_0}{V_0}}}{2}$
To calculate the area of triangle BOC,${A_2}$:
$\Rightarrow {A_2} = \dfrac{1}{2} \times b \times h$
where b = base of triangle and h = height.
Base, $b = 2{V_0} - {V_0} = {V_0}$
Height, $h = 3{p_0} - 2{p_0} = {p_0}$
Hence, area of BOC –
$\Rightarrow {A_2} = \dfrac{1}{2} \times {P_0} \times {V_0} = \dfrac{{{P_0}{V_0}}}{2}$
Since the triangle BOC is anti-clockwise, the work done is negative.
$\therefore {W_2} = {A_2} = - \dfrac{{{P_0}{V_0}}}{2}$
Total work done = ${W_1} + {W_2} = \dfrac{{{P_0}{V_0}}}{2} + \left( { - \dfrac{{{P_0}{V_0}}}{2}} \right) = 0$
Therefore, the work done is equal to 0.
Hence, the correct option is Option D.
Note: When two quantities in general, are plotted on a graph such as A v/s B, the following rules are applicable:
1. The product AB is represented by the area under the curve.
2. The ratio $\dfrac{A}{B}$ represents the slope of the tangent at each point on the curve.
Work done, $W = PV$
Hence, we consider the area under the curve of a P-V graph.
Complete step by step solution:
The work done is defined as the product of the force and the displacement.
$W = Fs$
The pressure is defined as the force per unit area.
$P = \dfrac{F}{A}$
If we consider a gas at a pressure P in a container of cross-section area A, the force exerted is given by –
$F = PA$
Substituting the force in the work done, we get –
$W = PAs$
The product of the area of cross-section of the container of the gas and the distance it travels horizontally, is equal to the volume swept by the gas.
Volume, $V = As$
Hence, the work done is given by –
$W = PV$
Since the work done is the product of pressure and volume, if we plot a graph of pressure and volume of the gas, the area under the curve will be equal to the work done.
If the graph is clockwise, the work is done on the system and its value is positive. If the graph is anti-clockwise, the work done by the system and the value is negative.
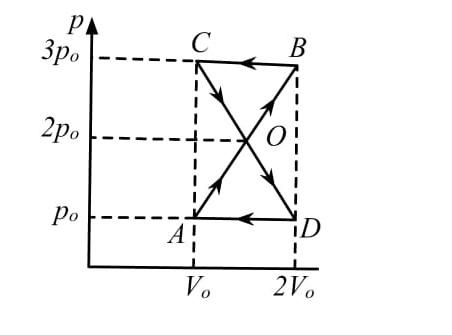
Consider a P-V graph as shown:

Work done in the entire process = Area of figure ADOBC
Area of figure ADOBC = Area of triangle AOD + Area of triangle BOC
To calculate the area of triangle AOD, ${A_1}$:
${A_1} = \dfrac{1}{2} \times b \times h$
where b = base of triangle and h = height.
Base, $b = 2{V_0} - {V_0} = {V_0}$
Height, $h = 2{p_0} - {p_0} = {p_0}$
Hence, area of AOD –
$\Rightarrow {A_1} = \dfrac{1}{2} \times {P_0} \times {V_0} = \dfrac{{{P_0}{V_0}}}{2}$
Since the triangle AOD is clockwise, the work done is positive.
$\therefore {W_1} = {A_1} = \dfrac{{{P_0}{V_0}}}{2}$
To calculate the area of triangle BOC,${A_2}$:
$\Rightarrow {A_2} = \dfrac{1}{2} \times b \times h$
where b = base of triangle and h = height.
Base, $b = 2{V_0} - {V_0} = {V_0}$
Height, $h = 3{p_0} - 2{p_0} = {p_0}$
Hence, area of BOC –
$\Rightarrow {A_2} = \dfrac{1}{2} \times {P_0} \times {V_0} = \dfrac{{{P_0}{V_0}}}{2}$
Since the triangle BOC is anti-clockwise, the work done is negative.
$\therefore {W_2} = {A_2} = - \dfrac{{{P_0}{V_0}}}{2}$
Total work done = ${W_1} + {W_2} = \dfrac{{{P_0}{V_0}}}{2} + \left( { - \dfrac{{{P_0}{V_0}}}{2}} \right) = 0$
Therefore, the work done is equal to 0.
Hence, the correct option is Option D.
Note: When two quantities in general, are plotted on a graph such as A v/s B, the following rules are applicable:
1. The product AB is represented by the area under the curve.
2. The ratio $\dfrac{A}{B}$ represents the slope of the tangent at each point on the curve.
Recently Updated Pages
Uniform Acceleration Explained: Formula, Examples & Graphs

JEE Main 2026 Session 1 Correction Window Started: Check Dates, Edit Link & Fees

AP EAPCET 2026 Exam Dates (OUT), Eligibility, Syllabus, Result, and Counselling

JEE Main 2026 Exam Pattern Released: Total Questions, and Marks, and Marking Scheme

JEE Main 2026 Admit Card Release Date, Exam Dates, & Download Link

JEE Main Marks Vs Percentile 2026: Calculate Percentile Based on Marks

Trending doubts
JEE Main 2026: City Intimation Slip and Exam Dates Released, Application Form Closed, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26




