Question

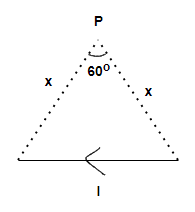
A straight wire of finite length carrying current I subtend an angle of \[60^\circ \] at point P as shown. The magnetic field at P is:

A) \[\dfrac{{\mathop \mu \nolimits_0 I}}{{2\sqrt 3 \pi x}}\]
B) \[\dfrac{{\mathop \mu \nolimits_0 I}}{{2\pi x}}\]
C) \[\dfrac{{\mathop {\sqrt 3 \mu }\nolimits_0 I}}{{2\pi x}}\]
D) \[\dfrac{{\mathop \mu \nolimits_0 I}}{{3\sqrt 3 \pi x}}\]

Answer 1

Hint: This given problem can be solved by taking the consideration of the magnetic field due to finite long straight wire carrying current I throughout the wire.

Complete step by step solution:
Step 1: As it is given in the question a straight wire of finite length carrying current I subtend an angle of \[60^\circ \] at point P.

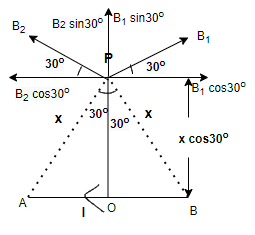
As shown in above figure, the magnetic field at point P will be the total magnetic field produced by point A and point B.
We can calculate the length PO by taking the consideration of right angle triangle and trigonometric angles such as \[\cos \theta = \]Adjacent/ hypotenuse
So, \[\cos \theta = \dfrac{{PO}}{{AP}}\]
\[PO = AP\cos \theta \] (1)
Where, \[AP = x\] and \[\theta = 30^\circ \]
After keeping all the values in above equation (1), we will get –
\[PO = x\cos 30^\circ \] (2)
Step 2: Now, we have to calculate the magnetic field due to a straight current carrying conductor of finite length at a point P, perpendicular distance PO from the linear conductor AB is given by –
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}\dfrac{I}{{PO}}\left( {\sin \mathop \phi \nolimits_1 + \sin \mathop \phi \nolimits_2 } \right)\] (3)
Where, \[\mathop \phi \nolimits_1 = \mathop \phi \nolimits_2 = 30^\circ \] and \[PO = x\cos 30^\circ \]
So, after keeping the all values in above equation (3), we will get –
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}\dfrac{I}{{x\cos 30^\circ }}\left( {\sin 30^\circ + \sin 30^\circ } \right)\] on further solving this equation
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}\dfrac{I}{{x\cos 30^\circ }}\left( {2\sin 30^\circ } \right)\]
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}\dfrac{{I\left( {2\sin 30^\circ } \right)}}{{x\cos 30^\circ }}\] on further simplifying this equation
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{4\pi }}\dfrac{I}{x}2\tan 30^\circ \] as we know that \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] so keeping this value in the equation
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{2\pi }}\dfrac{I}{x}\dfrac{1}{{\sqrt 3 }}\] on rearranging this equation
\[B = \dfrac{{\mathop \mu \nolimits_0 }}{{2\sqrt 3 \pi }}\dfrac{I}{x}\]
So, the magnetic field at point P will be \[B = \dfrac{{\mathop \mu \nolimits_0 }}{{2\sqrt 3 \pi }}\dfrac{I}{x}\].

So, the correct option is (A).

Note:
(i) As current is flowing in the conductor from B to A, the direction of magnetic field is normal to the plane of conductor downwards.
(ii) If the direction is opposite i.e. from the A to B, then the direction of the magnetic field is normal to the plane of conductor upwards.