Question

A small girl of height 1m can just see her image in a vertical plane mirror 4m away from her. Her eyes are 0.92m from the floor. In order that she sees her full image in the mirror, the shortest vertical dimension of the mirror is
(A)$0.50m$
(B)$0.70m$
(C)$0.46m$
(D)$0.56m$

Answer 1

Hint: The minimum length of the mirror will be the length of the mirror which is sufficient to make the light through the head and feet of the person reach the person’s eyes. Angle of incidence and angle of reflection are the same in magnitude.

Formula used:
\[\angle i = \angle r\]
\[\angle i\]is angle of incidence and \[\angle r\]is angle of reflection.

Complete Step-by-step solution:

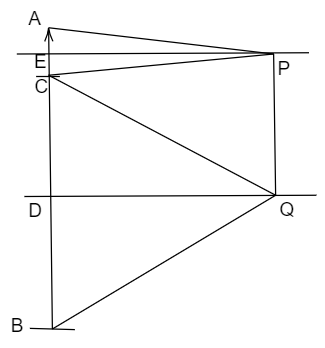
In the figure,
AB is the girl, PQ is the mirror, A is the topmost point on her head, B is the bottom-most part of her feet which are on the ground, C is the point on AB where her eyes are located, P and Q are the endpoints of the mirror. E and D are the points of intersection of the line representing the girl and the normal from the point where light through the head and feet of the person reach the person’s eyes i.e. line perpendicular to PQ from P and Q.
\[AB = 1m\], \[PE = QD = 4m\], \[BC = 0.92m\]
\[ \Rightarrow \angle i = \angle r\]
\[\angle i\]is angle of incidence and \[\angle r\]is angle of reflection.
Hence,
$\angle APE = \angle EPC = x$ and $\angle DQC = \angle BQD = y$
$ \Rightarrow AB = AC + BC$
So,$AC = 0.08m$
 We can assert that $\tan x = \dfrac{{AE}}{{EP}}$
Similarly,
In $\Delta CPE$,$\Delta BQD$ and$\Delta DQC$ that $\tan x = \dfrac{{CE}}{{EP}}$,$\tan y = \dfrac{{BD}}{{DQ}}$,$\tan y = \dfrac{{CD}}{{DQ}}$
From the above equations, we can assert that,
$AE = CE = a$ and $BD = CD = b$
From the figure, we can assert that the minimum length of the mirror is $a + b$.
\[a = \dfrac{1}{2}AC = 0.04m\] and \[b = \dfrac{1}{2}BC = 0.46m\]
Hence,
$a + b = 0.50m$

The correct answer is (A)$0.50m$

Note:
In a right angle triangle $\Delta ABC$ right angled at B then $\tan (\angle C)$ will be equal to $\dfrac{{AB}}{{BC}}$. The above question is a very popular question hence one must remember that the minimum length of mirror required is half the height of the person viewing in the mirror.