Question

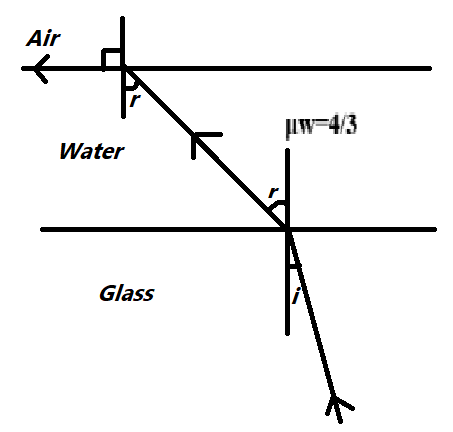
A ray of light is incident at the glass-water interface at an angle i. It merges finally parallel to the surface of the water. Then, the value of ${\mu _g}$ would be (where ${\mu _g}$ is the refractive index of glass with respect to water)

A. $\left( {\dfrac{4}{3}} \right)\sin i$
B. $\dfrac{1}{{(\sin i)}}$
C. $\dfrac{4}{3}$
D. $1$

Answer 1

Hint: Here in this question, given that a ray of light is incident through glass medium to the water medium at an angle i and merges parallel to the surface of water. Here we have to find the value of ${\mu _g}$ . As we know that we can easily find the solution using Snell’s law.


Formula used:
 Snell’s law
${}_g^w\mu = \dfrac{{\sin r}}{{\sin i}}$

Complete answer:
As we know that by applying the Snell’s law, we can easily find the solution of the question,
By applying the Snell’s law at the position of Glass-water surface,
${}_g^w\mu = \dfrac{{\sin r}}{{\sin i}}$
Here, $w$ stands for water and $g$ stands for glass,
As by putting the value we get the value as,
${}_g^w\mu = \dfrac{{\sin r}}{{\sin i}} = \dfrac{{{}_g\mu }}{{{}_w\mu }}....(i)$
As we take the above equation as equation(i)
Now, Applying the Snell’s law at the position of water-air surface,
${}_w^a\mu = \dfrac{{\sin {{90}^ \circ }}}{{\sin r}}$
Here, $a$ stands for air and $w$ stands for water,
By putting the whole value in above equation, we get,
${}_w^a\mu = \dfrac{{\sin {{90}^ \circ }}}{{\sin r}} = \dfrac{{{}_w\mu }}{{{}_a\mu }}....(ii)$
Now, by multiplying equation(i) with equation(ii) we get,
$\dfrac{{{}_g\mu }}{{{}_a\mu }} = \dfrac{1}{{\sin i}}$
By taking the whole conclusion we get,
${}_g\mu = \dfrac{1}{{\sin i}}$
Therefore, the correct answer for the value of ${}_g\mu $ is $\dfrac{1}{{\sin i}}$ .
Hence, the correct option is (B).


Note:
Snell's law often applies to isotropic or specular material only (such as glass). The ordinary or o-ray, which obeys Snell's law, and the other extraordinary or e-ray, which may not be co-planar with the incident ray, can be separated by birefringence in anisotropic media, such as certain crystals. So, check the material before using the formula.