Question

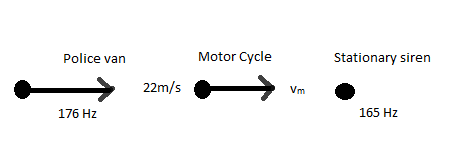
A police car moving at 22 m/s, chases a motorcyclist. The policeman sounds his horn at 176 Hz, while both of them move towards a stationary siren of frequency 165 Hz as shown in the figure. If the motorcyclist does not observe any beats, his speed must be: (take the speed of sound = 330 m/s)

A) 33 m/s
B) 22 m/s
C) zero
D) 11 m/s

Answer 1

Hint: Frequency is defined as the number of waves that pass through a fixed point in the unit of time. It is also defined as the number of oscillations per unit of time. The unit of frequency is Hertz.

Complete step by step solution:
Given data:
Speed of a police car, ${v_s} = 22m/s$
Frequency of the sound horn, ${n_{car}} = 176Hz$
Frequency of the siren, ${n_{siren}} = 165Hz$
Speed of the sound, v = 330 m/s
Speed of the motorcyclist, ${v_m}$ =?
 It is given that in the first case the police car which is a source of sound is moving at a speed ${v_s}$and is approaching a motorcycle (observer) which in turn is moving away from the police car with a speed of ${v_m}$.
Thus the apparent frequency of the sound heard by the motorcyclist is given by,
$\Rightarrow n' = {n_{car}}\left( {\dfrac{{v - {v_m}}}{{v - {v_s}}}} \right)\_\_\_\_\_\_\_\left( 1 \right)$
Again in the second case the motorcyclist, an observer is approaching a stationary siren, source at a speed of ${v_m}$
Thus the apparent frequency of the sound heard by the motorcyclist is given by,
$\Rightarrow n'' = {n_{siren}}\left( {\dfrac{{v + {v_m}}}{v}} \right)\_\_\_\_\_\_\_\left( 2 \right)$
It is given that the motorcyclist does not observe any beats and this is possible only when the difference in the frequencies heard by the motorcyclist is zero.
Thus $n' - n'' = 0$
$ \Rightarrow n' = n''$
Substituting the values of $n'$ and $n''$ from the equations 1 and 2, we get,
$\Rightarrow {n_{car}}\left( {\dfrac{{v - {v_m}}}{{v - {v_s}}}} \right) = {n_{siren}}\left( {\dfrac{{v + {v_m}}}{v}} \right)$
Thus substituting the values of ${n_{car}},{v_m},{v_s},{n_{siren}},v,$ we get
$\Rightarrow 176\left( {\dfrac{{v - {v_m}}}{{330 - 22}}} \right) = 165\left( {\dfrac{{v + {v_m}}}{{330}}} \right)$
$ \Rightarrow \left( {\dfrac{{v - {v_m}}}{{v + {v_m}}}} \right) = \dfrac{{165}}{{176}} \times \dfrac{{308}}{{330}} = \dfrac{7}{8}$
$ \Rightarrow 8v - 8{v_m} = 7v + 7{v_m}$
$ \Rightarrow 15{v_m} = v$
$ \Rightarrow {v_m} = \dfrac{v}{{15}} = \dfrac{{330}}{{15}} = 22m/s$
Thus the speed of the motorcyclist $ = 22m/s$

Hence the correct option is B.

Note: The sound source generates the sound waves and creates the vibrations in the surrounding medium. As this continues the vibrations propagate away at the speed of the sound.