
A point object is placed at a distance of 12 cm on the axis of a convex lens of focal length 10 cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is:
A) 20 cm
B) 25 cm
C) 30 cm
D) 22 cm
Answer
228.9k+ views
Hint: In this problem, we are dealing with 2 different entities such as convex mirror and convex lens but the concepts dealing with the image formation is similar. There are two similar formulae: Mirror equation and Lens equation, which gives the relationship between the distances of the object and image and their focal lengths.
If u is the distance of the object from the pole and v is the distance of the image from the pole. We have:
Mirror equation: Focal length, $\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Lens equation: Focal length, $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Complete step by step answer:
Step 1: Consider the image formation by the lens.
Here is the ray diagram for the image formation:
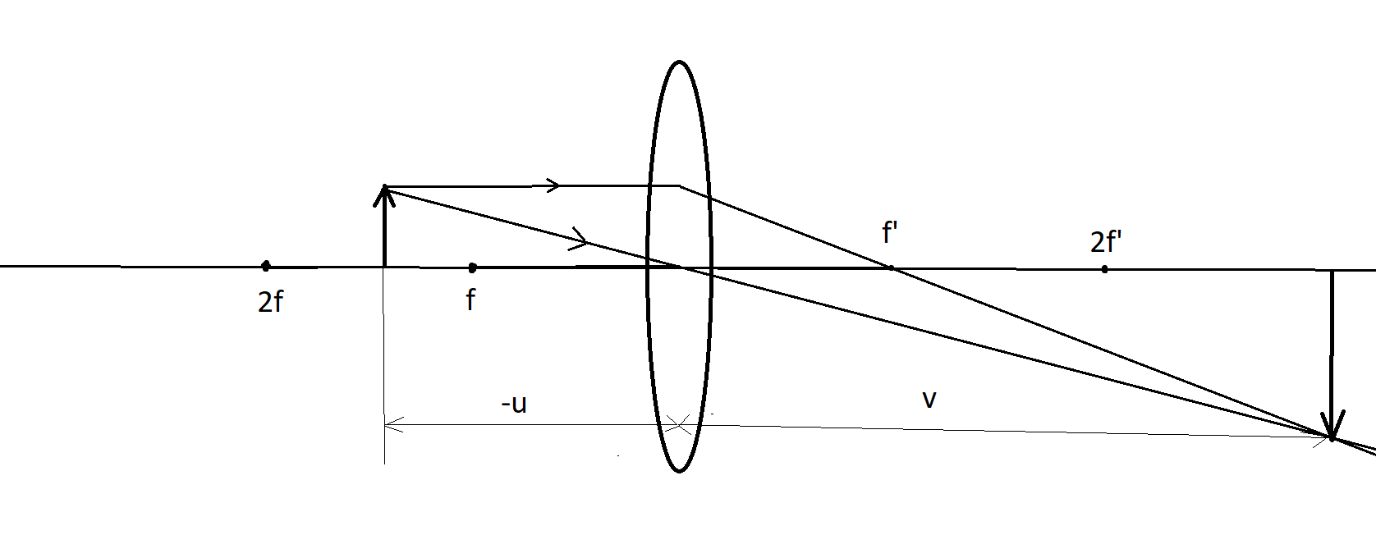 There are two rays emanating from the object:
i) The first ray passes parallel to the principal axis and after refraction, passes through the focal length.
ii) The second ray passes through the centre and goes undeviated.
There are two rays emanating from the object:
i) The first ray passes parallel to the principal axis and after refraction, passes through the focal length.
ii) The second ray passes through the centre and goes undeviated.
When they meet, the image is formed beyond the $2f'$.
Given,
Distance of object, (negative since it is opposite to movement of light), $u = - 12cm$
Focal length, $f = 10cm$
By applying the Lens equation to this case, we can obtain the distance of image from the lens.
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$\dfrac{1}{{10}} = \dfrac{1}{v} - \dfrac{1}{{\left( { - 12} \right)}}$
Solving for v:
$\dfrac{1}{v} = \dfrac{1}{{10}} - \dfrac{1}{{12}}$
$\dfrac{1}{v} = \dfrac{{12 - 10}}{{120}}$
So, $v = \dfrac{{120}}{2} = 60cm$
The image formed by the lens is at a distance of 60cm from the lens.
Step 2: Consider the image formed by mirror
For the convex mirror, the object is the image formed by the lens. But the convex mirror is at a distance of 10cm from the convex mirror and the image formed by the lens at 60cm from the lens.
Since the convex mirror is diverging, the image is formed by retracing the reflected rays and they coincide at the distance equal to difference between image formed by the lens and separation distance between lens and mirror.
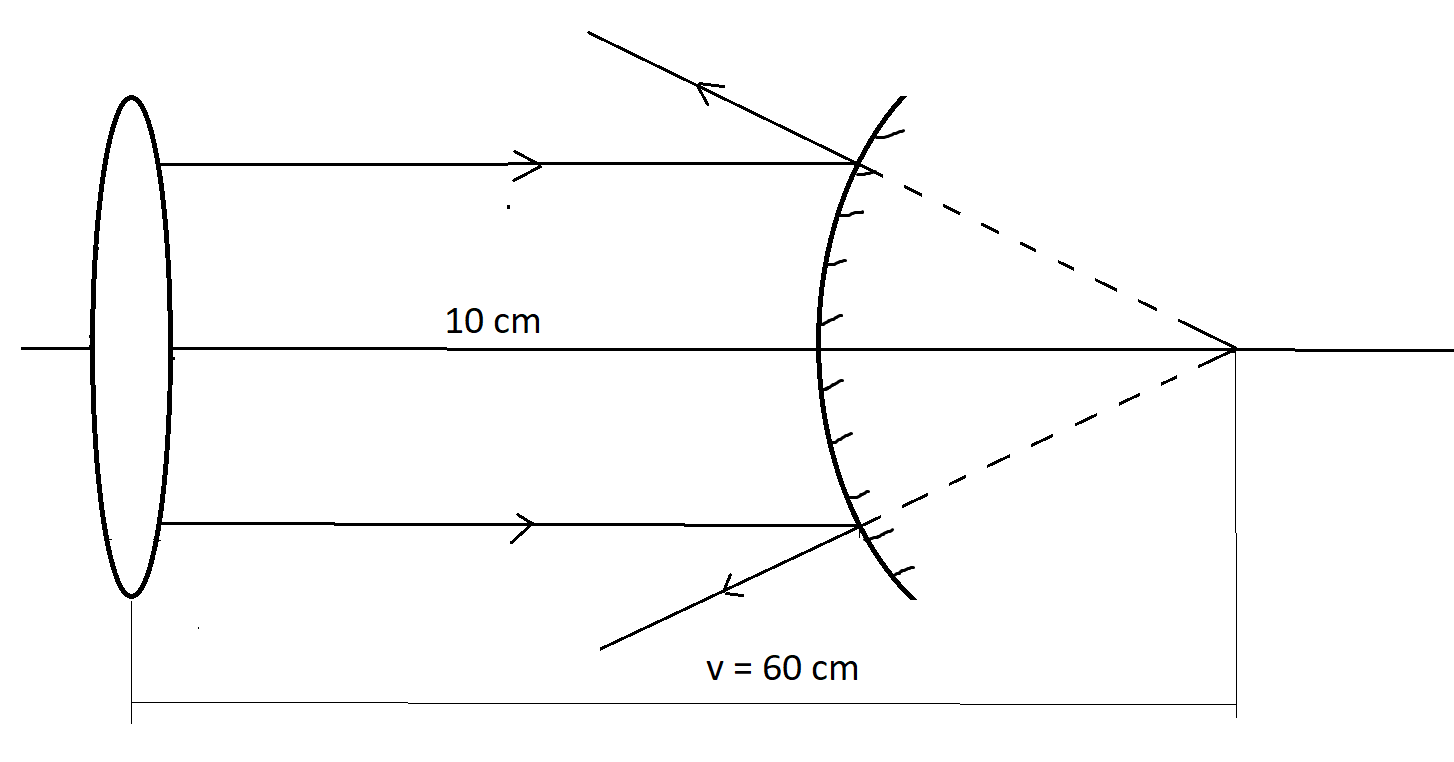
As per the above figure,
Distance from the convex mirror, d = Distance of image by lens – Distance of lens from mirror
$d = 60 - 10 = 50cm$
So, we can say that the image formed by the convex mirror is at a distance of 50 cm.
Step 3: Putting it together
Given that the image formed coincides with the object itself, it can only happen if the object is placed at the centre of curvature of the mirror.
Thus, we can say that :–
Radius of curvature, R = Image formed by convex mirror, d
$R = d$
$R = 50cm$
Now that we have the radius of curvature, the focal length is given by –
$f = \dfrac{R}{2} = \dfrac{{50}}{2} = 25cm$
Focal length of the convex mirror, f = 25 cm
Hence, the correct option is Option (B).
Note: While applying the lens formula or mirror formula, students can often make a mistake in the signs. There is no need to worry since there is a trick where you can verify your answer. If the focal length is asked in the question, it is convex if it is a positive sign and it is concave if it is a negative sign. So, when you get the focal length, cross-verify the sign of focal length with the type of mirror/lens to know if you are moving on the right path.
If u is the distance of the object from the pole and v is the distance of the image from the pole. We have:
Mirror equation: Focal length, $\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Lens equation: Focal length, $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Complete step by step answer:
Step 1: Consider the image formation by the lens.
Here is the ray diagram for the image formation:
 There are two rays emanating from the object:
i) The first ray passes parallel to the principal axis and after refraction, passes through the focal length.
ii) The second ray passes through the centre and goes undeviated.
There are two rays emanating from the object:
i) The first ray passes parallel to the principal axis and after refraction, passes through the focal length.
ii) The second ray passes through the centre and goes undeviated. When they meet, the image is formed beyond the $2f'$.
Given,
Distance of object, (negative since it is opposite to movement of light), $u = - 12cm$
Focal length, $f = 10cm$
By applying the Lens equation to this case, we can obtain the distance of image from the lens.
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$\dfrac{1}{{10}} = \dfrac{1}{v} - \dfrac{1}{{\left( { - 12} \right)}}$
Solving for v:
$\dfrac{1}{v} = \dfrac{1}{{10}} - \dfrac{1}{{12}}$
$\dfrac{1}{v} = \dfrac{{12 - 10}}{{120}}$
So, $v = \dfrac{{120}}{2} = 60cm$
The image formed by the lens is at a distance of 60cm from the lens.
Step 2: Consider the image formed by mirror
For the convex mirror, the object is the image formed by the lens. But the convex mirror is at a distance of 10cm from the convex mirror and the image formed by the lens at 60cm from the lens.
Since the convex mirror is diverging, the image is formed by retracing the reflected rays and they coincide at the distance equal to difference between image formed by the lens and separation distance between lens and mirror.

As per the above figure,
Distance from the convex mirror, d = Distance of image by lens – Distance of lens from mirror
$d = 60 - 10 = 50cm$
So, we can say that the image formed by the convex mirror is at a distance of 50 cm.
Step 3: Putting it together
Given that the image formed coincides with the object itself, it can only happen if the object is placed at the centre of curvature of the mirror.
Thus, we can say that :–
Radius of curvature, R = Image formed by convex mirror, d
$R = d$
$R = 50cm$
Now that we have the radius of curvature, the focal length is given by –
$f = \dfrac{R}{2} = \dfrac{{50}}{2} = 25cm$
Focal length of the convex mirror, f = 25 cm
Hence, the correct option is Option (B).
Note: While applying the lens formula or mirror formula, students can often make a mistake in the signs. There is no need to worry since there is a trick where you can verify your answer. If the focal length is asked in the question, it is convex if it is a positive sign and it is concave if it is a negative sign. So, when you get the focal length, cross-verify the sign of focal length with the type of mirror/lens to know if you are moving on the right path.
Recently Updated Pages
Uniform Acceleration Explained: Formula, Examples & Graphs

States of Matter Chapter For JEE Main Chemistry

Young’s Double Slit Experiment Derivation Explained

Wheatstone Bridge – Principle, Formula, Diagram & Applications

Circuit Switching vs Packet Switching: Key Differences Explained

Mass vs Weight: Key Differences Explained for Students

Trending doubts
JEE Main 2026: Admit Card Out, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding the Electric Field of a Uniformly Charged Ring

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




