Question

A nichrome wire of uniform cross-sectional area is bent to form a rectangular loop ABCD. Another nichrome wire of the same cross-section is connected to form the diagonal AC. Find out the ratio of the resistance across BD and AC if AB=0.4m and BC=0.3m:
A) $\dfrac{{59}}{{35}}$.
B) $\dfrac{{35}}{{59}}$.
C) $\dfrac{{29}}{{17}}$.
D) $\dfrac{{17}}{{29}}$.

Answer 1

Hint: Resistivity of each material is always constant. The resistivity of the material is defined as the resistance of a wire which is $1m$ long and has $1{m^2}$ area of cross section. Different materials have different values of resistivity.

Formula used:
The formula of the resistivity is given by,
$R = \dfrac{{\rho \cdot l}}{A}$
Where R is the resistance $\rho $ is the density $l$ is the length of the wire and A is the cross sectional area of the

Complete step by step solution:
It is given in the problem that a nichrome wire of uniform cross-sectional area is bent in the shape of a loop which is ABCD another nichrome wire is taken and connected to the rectangular loop such that it forms a diagonal AC and BD.

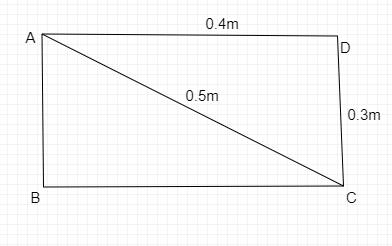
As the formula of the resistance is given by,
$R = \dfrac{{\rho \cdot l}}{A}$
Where R is the resistance $\rho $ is the density $l$ is the length of the wire and A is the cross sectional area of the
The ratio of the density and area of cross section is equal to,
$ \Rightarrow k = \dfrac{\rho }{A}$
This ratio is always constant and let the value of this ratio be equal to 10.
$\dfrac{\rho }{A} = 10$………eq. (1)
As resistance is given by$R = k \cdot l$, therefore the resistance of the wire AB, BC, CD and AC is given by,
${R_{AB}} = 4\Omega $, ${R_{BC}} = 3\Omega $,${R_{CD}} = 4\Omega $ and ${R_{AD}} = 3\Omega $.
The diagram of the of the new circuit is given by,

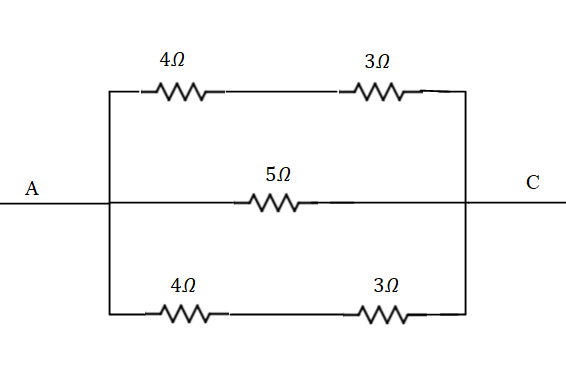
The equivalent resistance between the points A and C is given by,
$ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{7} + \dfrac{1}{5} + \dfrac{1}{7}$
$ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{17}}{{35}}\Omega $
$ \Rightarrow {R_{eq}} = \dfrac{{35}}{{17}}\Omega $.
$ \Rightarrow {R_{AC}} = \dfrac{{35}}{{17}}\Omega $
Now let us calculate the value of resistance across BD, to find the resistance across the BD we need to connect it to the battery.

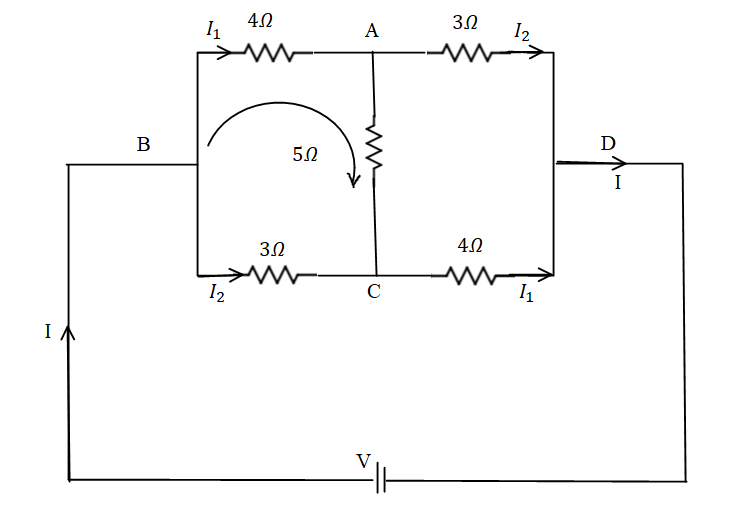
Applying Kirchhoff’s voltage law across BACB.
$ \Rightarrow - 4{I_1} - 5\left( {{I_1} - {I_2}} \right) + 3{I_2} = 0$
$ \Rightarrow {I_1} = \dfrac{8}{9}{I_2}$………eq. (1)
Applying the Kirchhoff’s voltage law in BADCB.
$ \Rightarrow V = 4{I_1} - 3{I_2}$
Replacing the value of ${I_1}$ in the above relation from equation (1) we get,
$ \Rightarrow V = 4{I_1} - 3{I_2}$
\[ \Rightarrow V = \left( {\dfrac{{59}}{9}} \right){I_2}\]………eq. (2)
Also,
$ \Rightarrow I = {I_1} + {I_2}$………eq. (3)
Solving equation (1), equation (2) and equation (3) and also use the relation$V = I \cdot {R_{eq.}}$.
$ \Rightarrow V = I \cdot {R_{eq.}}$
$ \Rightarrow \left( {\dfrac{{59}}{9}} \right){I_2} = I \cdot {R_{eq.}}$
$ \Rightarrow \left( {\dfrac{{59}}{9}} \right){I_2} = \left( {{I_1} + {I_2}} \right) \cdot {R_{eq.}}$
$ \Rightarrow \left( {\dfrac{{59}}{9}} \right){I_2} = \left( {\dfrac{8}{9}{I_2} + {I_2}} \right) \cdot {R_{eq.}}$
$ \Rightarrow \left( {\dfrac{{59}}{9}} \right){I_2} = \left( {\dfrac{{17}}{9}{I_2}} \right) \cdot {R_{eq.}}$
$ \Rightarrow \left( {\dfrac{{59}}{9}} \right) = \left( {\dfrac{{17}}{9}} \right) \cdot {R_{eq.}}$
$ \Rightarrow 59 = \left( {17} \right) \cdot {R_{eq.}}$
$ \Rightarrow {R_{eq.}} = \dfrac{{59}}{{17}}\Omega $
The resistance across the resistance BD is equal to ${R_{BD}} = \dfrac{{59}}{{17}}\Omega $
Let us divide the resistance across BD and AC is given by,
$ \Rightarrow \dfrac{{{R_{BD}}}}{{{R_{AC}}}} = \dfrac{{\left( {\dfrac{{59}}{{17}}} \right)}}{{\left( {\dfrac{{35}}{{17}}} \right)}}$
$ \Rightarrow \dfrac{{{R_{BD}}}}{{{R_{AC}}}} = \dfrac{{59}}{{35}}$.

The ratio of resistance of the BD and AC is equal to $\dfrac{{{R_{BD}}}}{{{R_{AC}}}} = \dfrac{{59}}{{35}}$. The correct answer for this problem is option A.

Note: It is advisable to students to remember the formula of the resistance as it can be used to solve the problems like these. Resistivity is different for different materials and therefore the material for making wire is chosen such that it has least value of resistivity.