Question

A loop made of straight edges has six corners at A (0, 0, 0), B (L, 0, 0), C(L, L, 0), D (0, L, 0), E (0, L, L) And F (0, 0, L). A magnetic field $\overrightarrow B = B_0 ​(\widehat{i}+ \widehat{k})T$ is present in the region. The flux passing through the loop ABCDEFA (in the order ) is:
A) \[{B_0}{L^2}Wb\]
B) \[2{B_0}{L^2}Wb\]
C) \[\sqrt 2 {B_0}{L^2}Wb\]
D) \[4{B_0}{L^2}Wb\]

Answer 1

Hint: The number of magnetic field lines passing through the given closed surface is called Magnetic flux. It is denoted by $\phi $ and the unit is Weber. The magnetic flux indicates the strength of magnetic lines that are produced by a magnet.

Complete step by step solution:
Let say L=1 the diagram will be like:

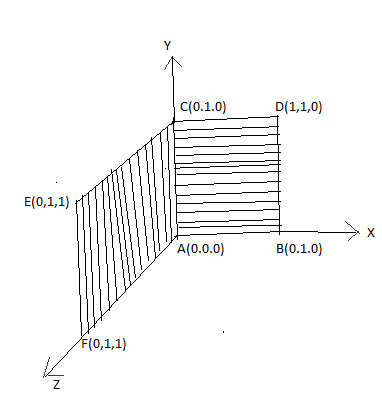
Given six corners are A (0, 0, 0), B (L, 0, 0), c (L, L, 0), D (0, L, 0), E (0, L, L) and F (0, 0, L).
Magnetic field, \[\overrightarrow B = {B_0}\left( {\widehat i + \widehat k} \right)T\]
Magnetic flux =?
The area vector of ABCD $ = {L^2}\widehat k$
The area vector of DEFA $ = {L^2}\widehat i$
Thus total area vector, \[\overrightarrow A = {L^2}\left( {\widehat i + \widehat k} \right)\]
We know that magnetic flux is given by the formula, $\phi = \overrightarrow B .\overrightarrow A $
Substituting the values of \[\overrightarrow B\] and \[\overrightarrow A \], we get,
\[\phi = {B_0}\left( {\widehat i + \widehat k} \right).{L^2}\left( {\widehat i + \widehat k} \right)\]
\[ \Rightarrow \phi = {B_0}{L^2}\left( {1 + 1} \right) = 2{B_0}{L^2}Wb\]
Thus the total magnetic flux, \[\phi = 2{B_0}{L^2}Wb\]

Hence the correct option is B.

Note: 1. The magnetic flux in the open surface is not zero and through a closed surface is zero always. It always forms a closed loop. The magnetic flux depends on the area and the magnetic strength of the magnet.
2. Magnetic flux starts from the north pole and ends at the south pole and they will never intersect each other. The lines of forces that are parallel to each other and in the same direction will repel each other.
3. The region around a magnet where the moving charge experiences a force is called a magnetic field. It depends on the magnet.
4. A closed path in a circuit is called a loop. It is used for executing a set of statements repeatedly, till a particular condition is satisfied.