Question

A force of \[20{\rm{ }}N\] is applied on a body of mass \[5{\rm{ }}kg\] resting on a horizontal plane. The body gains kinetic energy of \[10{\rm{ }}joules\] after it moves a distance of \[2{\rm{ }}m\]. The frictional force is:
1. \[10N\]
2. \[15N\]
3. \[20N\]
4. \[30N\]

Answer 1

Hint: To solve this question we should first start with the free body diagram so that will understand all kinds of forces acting on it. In this question, we will use the concept of kinetic energy to find the velocity of the block.

Formula Used:
\[K.E. = \dfrac{1}{2}m{v^2}\]
\[{v^2} = {u^2} + 2as\]
\[f = F - ma\]

Complete answer:
Given Data:
Force \[ = 20N\]
Mass of the body \[ = 5kg\]
Kinetic energy gained by the body on the horizontal surface after moving \[2{\rm{ }}m\] \[ = 10J\]

Now, let us draw a free body diagram for a better understanding of the concept,

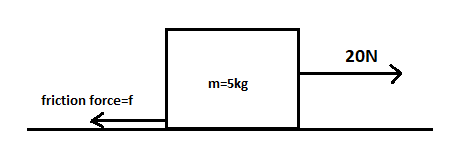
So, from the above figure, we can see that both forces applied and the force of friction are opposite to each other in direction as shown in the above figure.

Now, we have to calculate frictional force from the above-given data:
Using the formula for K.E. we get
\[K.E. = \dfrac{1}{2}m{v^2}\]
\[ \Rightarrow 10J = \dfrac{1}{2} \times 5kg \times {v^2}\]
\[ \Rightarrow {v^2} = 4\]
\[\therefore v = 2m/s\]

For finding out frictional force we need the velocity of the box, now for finding acceleration we have to use a kinematic equation and that is given by:
\[{v^2} = {u^2} + 2as\]
\[u\] is the initial velocity and it is zero since the box was at rest, \[s\] is the distance the box is pushed i.e., \[2{\rm{ }}m\]

Therefore, after putting all the values in the above equation, we get
\[ \Rightarrow 4 = 0 + 2a(2)\]
\[ \Rightarrow a = 1m/{s^2}\]

Now, we have a formula for the frictional force
\[f = F - ma\]
\[ \Rightarrow f = 20N - 5kg \times 1m/{s^2}\]
\[ \Rightarrow f = 20N - 5N\]
\[\therefore f = 15N\]
Thus, the frictional force acting on the box is \[15N\]

Therefore, the right answer is option 2.

Note: We should remember that we can not always use the kinetic energy formula to find the velocity of the block. In this problem we had given the value of the kinetic energy thus we can use the formula to attain the required value of velocity.