Question

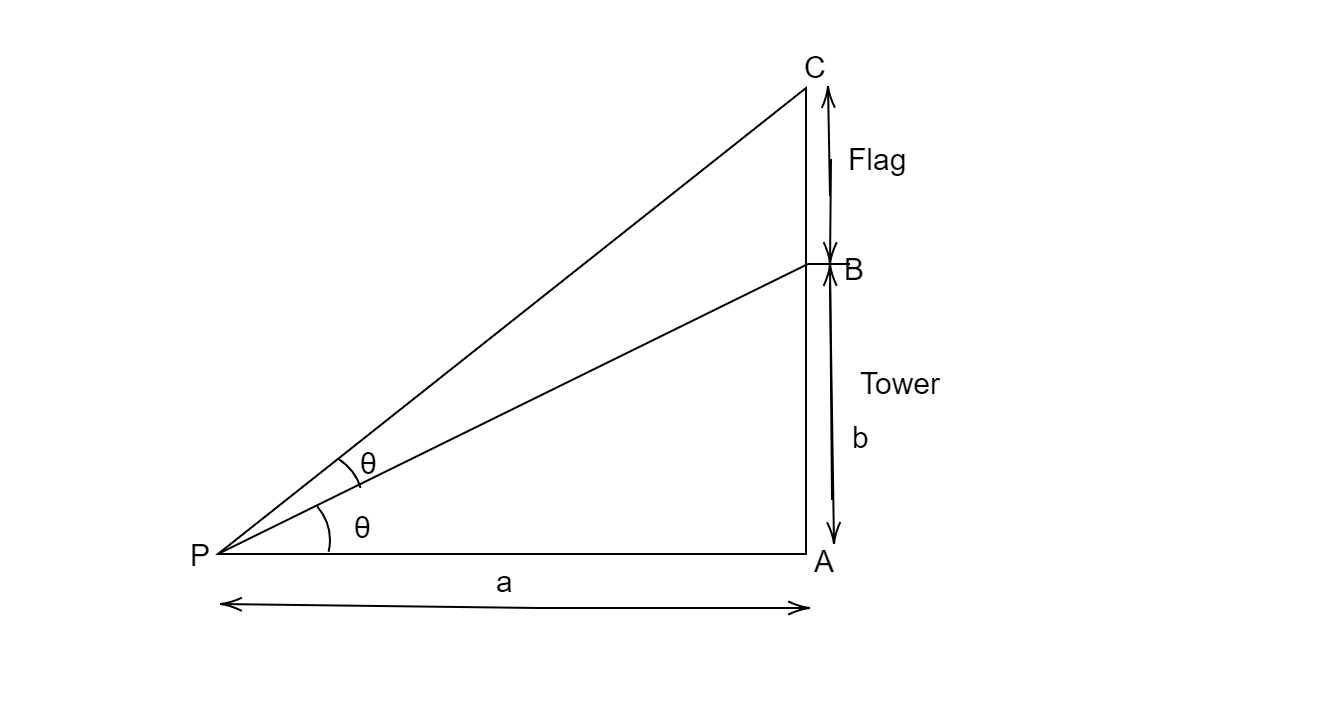
A flag is standing vertically on a tower of height $b$. On a point at a distance $a$ from the foot of the tower, the flag and the tower subtend equal angles. The height of the flag is
1. $b.\dfrac{{\left[ {{a^2} + {b^2}} \right]}}{{\left[ {{a^2} - {b^2}} \right]}}$
2. $a.\dfrac{{\left[ {{a^2} - {b^2}} \right]}}{{\left[ {{a^2} + {b^2}} \right]}}$
3. $b.\dfrac{{\left[ {{a^2} - {b^2}} \right]}}{{\left[ {{a^2} + {b^2}} \right]}}$
4. $a.\dfrac{{\left[ {{a^2} + {b^2}} \right]}}{{\left[ {{a^2} - {b^2}} \right]}}$

Answer 1

Hint:

In this question, the height of the tower is $b$ and the flag and the tower subtend equal angles at the distance $a$ from the foot of the tower. Let the height of the flag be any constant and use $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$ in both the required triangles. Solve further to calculate the height of the flag.



Formula used:
$\tan 2\theta = \dfrac{{2\tan \theta }}{{\left[ {1 - {{\tan }^2}\theta } \right]}}$
Trigonometric ratio –
$\tan \theta = \dfrac{{Perpendicular}}{{Base}}$



Complete step by step solution: 

Given that,
Height of the tower $ = b$
And the flag and the tower subtend equal angles at the distance $a$ from the foot of the tower
$ \Rightarrow \angle CPB = \angle BPA = \theta $, $PA = a$
Also, let the height of the tower be $x$
In $\Delta BPA$,
$\dfrac{b}{a} = \tan \theta - - - - - \left( 1 \right)$
In $\Delta CPA$
$\dfrac{{b + x}}{a} = \tan 2\theta $
$\dfrac{{b + x}}{a} = \dfrac{{2\tan \theta }}{{\left[ {1 - {{\tan }^2}\theta } \right]}}$
From equation (1)
$\dfrac{{b + x}}{a} = \dfrac{{2\left( {\dfrac{b}{a}} \right)}}{{\left[ {1 - \left( {\dfrac{{{b^2}}}{{{a^2}}}} \right)} \right]}}$
$\dfrac{{b + x}}{a} = \dfrac{{\left( {\dfrac{{2b}}{a}} \right)}}{{\left( {\dfrac{{{a^2} - {b^2}}}{{{a^2}}}} \right)}}$
$\dfrac{{b + x}}{a} = \dfrac{{2ab}}{{{a^2} - {b^2}}}$
$b + x = \dfrac{{2{a^2}b}}{{{a^2} - {b^2}}}$
$x = \dfrac{{2{a^2}b}}{{{a^2} - {b^2}}} - b$
$x = \dfrac{{2{a^2}b - b{a^2} + {b^3}}}{{{a^2} - {b^2}}}$
$x = \dfrac{{{a^2}b + {b^3}}}{{{a^2} - {b^2}}}$
$x = b.\left( {\dfrac{{{a^2} + {b^2}}}{{{a^2} - {b^2}}}} \right)$
Thus, the height of the flag is $b.\left( {\dfrac{{{a^2} + {b^2}}}{{{a^2} - {b^2}}}} \right)$
Hence, option (1) is the correct answer i.e., $b.\dfrac{{\left[ {{a^2} + {b^2}} \right]}}{{\left[ {{a^2} - {b^2}} \right]}}$.
Note: The key concept involved in solving this problem is the good knowledge of applications of trigonometry. Students must know that trigonometry is one of the branches, which teaches us about the relationships between angles and sides of a triangle. To solve such questions, try to use $\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}},\cos \theta = \dfrac{{Base}}{{Hypotenuse}},\tan \theta = \dfrac{{Perpendicular}}{{Base}}$ these formula in the required triangles or their reciprocals.


Hence, Option (2) is the correct answer.

Note: The key concept involved in solving this problem is the good knowledge of quadratic equations. Students must know that if roots are given then we can directly find the equation using ${x^2} - Px + Q = 0$ where $P$ and $Q$ are the sum and product of the roots respectively. Likewise, if the equation is given as $a{x^2} + bx + c = 0$and we have to find the sum and product of roots we can find directly using Sum of roots $ = \dfrac{{ - b}}{a}$ and product $ = \dfrac{c}{a}$.