Question

A electron ($q=1.6\times {{10}^{-19}}C$) is moving at the right angle to the uniform magnetic field $3.534\times {{10}^{-5}}T$. The time taken by the electron to complete a circular orbit is [MH CET $2004$]
A.$2$$\mu s$
B.$4$$\mu s$
C.$3$$\mu s$
D.$1$$\mu s$

Answer 1

Hint: A charged electron is moving at the right angle to the uniform magnetic field following a circular path, then it experiences a force in a perpendicular direction to the direction of the current and magnetic field. The time is taken by the electron to complete a circle of circumference $2\pi r$moving with velocity $v$.

Formula used:
Time,$T$ for the electron to complete a circular path,
$T=\dfrac{2\pi m}{qB}$
Here $m\And q$are the mass and charge of an electron. $B$is a uniform magnetic field.


Complete answer:

When a particle carrying charge $q$ moves in the presence of a uniform magnetic field ($\vec{B}$) the magnetic force $\vec{F}$ becomes perpendicular to the velocity $\vec{v}$ of the particle. In the magnetic field, a particle follows a circular path.

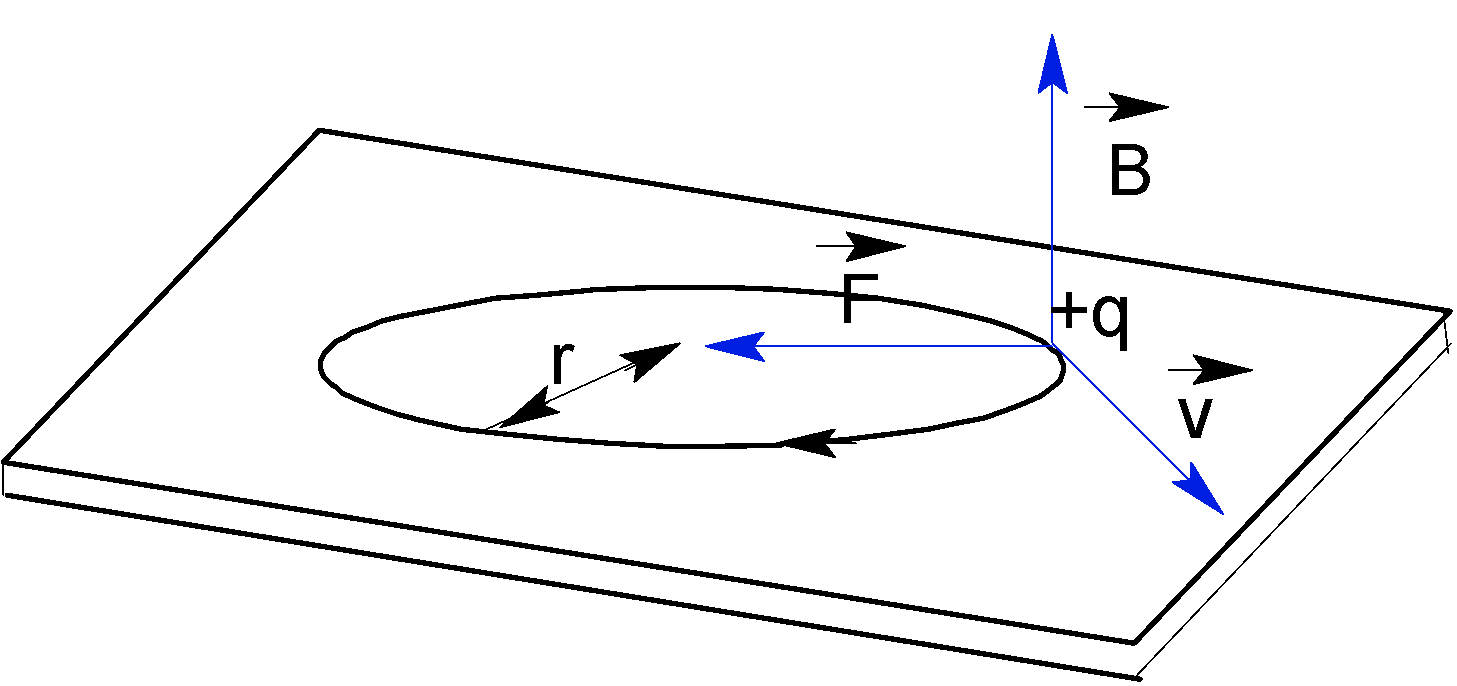
Hence radius of the circular path can be written as,
$r=\dfrac{mv}{qB}$
Or,$\dfrac{r}{v}=\dfrac{m}{qB}$ …….(i)
Period,$T$ of the motion taken by a charged particle to complete one circle of circumference $2\pi r$ moving with velocity $v$.
$T=\dfrac{2\pi r}{v}$ ……..(ii)
Putting the $\dfrac{r}{v}$values in equation (ii),
$T=2\pi \times \dfrac{m}{qB}$
Or,$T=\dfrac{2\pi m}{qB}$ ……..(iii)
Given $q=1.6\times {{10}^{-19}}C$,$B=3.534\times {{10}^{-5}}T$
And we know the mass of the electron,$m=9.1\times {{10}^{-31}}kg$
$\therefore T=\dfrac{2\times 3.14\times 9.1\times {{10}^{-31}}}{1.6\times {{10}^{-19}}\times 3.534\times {{10}^{-5}}}=1.01\times {{10}^{-6}}\sec $
Or,$T=1\mu s$
Therefore, the time taken by the electron to complete a circular orbit is $1$$\mu s$.

Thus, option (D) is correct.


Note: The time taken by the electron does not depend on speed. If two electrons enter the magnetic field at different speeds will complete a circular orbit with different radii such that the radius-to-velocity radius ratio is the same for both of them. Faster particles will have to traverse larger circular orbits then both of them will take the same time to complete a circular orbit.