Question

A current of 1A is flowing on the side of an equilateral triangle of side \[4.5\times {{10}^{-2}}m\]. The magnetic field at the centre of the triangle will be:
A) $4\times {{10}^{-5}} {Wb}/m^2$
B) $Zero$
C) $2\times {{10}^{-5}} {Wb}/m^2$
D) $8\times {{10}^{-5}} {Wb}/m^2$

Answer 1

Hint: Magnetic field due to current carrying conductor (wire) is, $B=\dfrac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)$.
Where r is the perpendicular distance from the wire of that point,
${{\phi }_{1}}$ and ${{\phi }_{2}}$ are angles.

Complete step by step solution:
When a current flows in a conductor or wire then produces a magnetic field around it. The magnetic field lines shape depend on the shape of the current carrying conductor. If the conductor is in the shape of a cylinder, then the magnetic field lines are circular around the wire (cylinder shape).
The magnetic field due to a finite conducting wire,
$B=\dfrac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)$
Where r is the perpendicular distance from the wire of that point,
${{\phi }_{1}}$ and ${{\phi }_{2}}$ are the angels.
For equilateral triangle
${{\phi }_{1}}={{\phi }_{2}}={{60}^{\circ }}$
$\Rightarrow \tan 30{}^\circ =\dfrac{r}{2.25\times {{10}^{-2}}}$

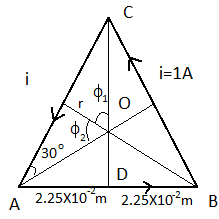
$r=2.25\times {{10}^{-2}}\times \tan 30{}^\circ $
$\Rightarrow r=2.25\times {{10}^{-2}} \times \dfrac{1}{\sqrt{3}}m$
Magnetic field at the centre of the triangle due side AB,
$\Rightarrow$ \[{{B}_{1}}=\dfrac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)\]
Direction of the magnetic field above the plane
Magnetic field is same due to side BC and CA and direction also same,
So resultant magnetic field
$B=3{{B}_{1}}=3\dfrac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)$
$\because {{\phi }_{1}}={{\phi }_{2}}={{60}^{\circ }}$
$\Rightarrow B=3\times \dfrac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{60}^{\circ }}+\sin {{60}^{\circ }} \right)$
$\Rightarrow B=3\times \dfrac{{{\mu }_{0}}i}{4\pi r}\left( \dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2} \right)$
$\Rightarrow B=3\times {{10}^{-7}}\times \dfrac{1}{\dfrac{2.25\times {{10}^{-2}}}{\sqrt{3}}}\left( \dfrac{\sqrt{3}+\sqrt{3}}{2} \right)$
$\Rightarrow B=\dfrac{\sqrt{3}\times {{10}^{-7}}\times \sqrt{3}}{2.25\times {{10}^{-2}}}$
$\Rightarrow B=\dfrac{9\times {{10}^{-7}}}{2.25\times {{10}^{-2}}}$
$\Rightarrow B=4\times {{10}^{-5}}$ ${Weber}/{{{\left( meter \right)}^{2}}}$

Note: When we find out the magnetic field at the centre, then maximum times we take the distance from the corner but really. We should take a perpendicular distance from the write to that point.