Question

A charge $q_1$ is revolving around a circle with charge $q_2$ at its centre. Find the speed of charge $q_1$.

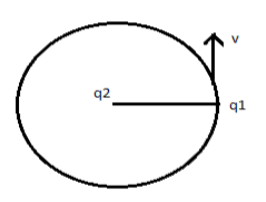
Answer 1

Hint: When the motion is circular then the centripetal force comes into play and it is a charge then electrostatic force also being generated.
Centripetal force is given as:
$\dfrac{{m{v^2}}}{R}$(m is the mass of the body, R is the radius of the circular region, v is the velocity)
Electrostatic force is given by:
$\dfrac{{qQ}}{{4\pi {R^2}}}$(q and Q are the charges R is the radius)
Using the above two forces we will solve this problem.

Complete step by step solution:
Let us discuss the centripetal force and electrostatic force in detail.
Centripetal force is defined as the force that is necessary to keep an object moving in a curved path and that is directed inward towards the centre of rotation. It is always directed orthogonally to the motion of the body and towards the fixed point of the instantaneous centre of curvature of the path.
Electrostatic force: Electrostatic force is the attractive or repulsive forces between the charged particles. When the charges are both of same polarity they repel each other and when the charges are of opposite polarity they attract each other.
Now we come to the calculation part.
We assume the charges like polarity and thus the electrostatic force will be repulsive in nature.
The force which is generated between the two charges is electrostatic and it is given by:
${F_e} = \dfrac{{KQq}}{{{R^2}}}$
Charge is revolving around the circular path, then centripetal force also comes into play which is given as:
$\Rightarrow \dfrac{{m{v^2}}}{R}$
Both the forces are balancing each other because one is acting outwards and the other is acting inwards, thus we can equate the two forces.
$ \Rightarrow \dfrac{{KQq}}{{{R^2}}} = \dfrac{{m{v^2}}}{R}$................(1)
We will cancel the common terms from equation 1
$ \Rightarrow {v^2} = \dfrac{{KQq}}{{Rm}}$
$ \Rightarrow v = \sqrt {\dfrac{{K{q_1}{q_2}}}{{Rm}}} $ velocity of charge $q_1$ .

Note: We have many applications of centripetal force such as the turn we take while driving a car, scooter or bicycle, planets revolving around the sun, bucket tied to a string. Electrostatic force has application in Van de Graff generators, photocopiers, laser printers and inkjet printers.