Question

A body performs S.H.M. Its kinetic energy KE varies with time t as indicated by graph
A.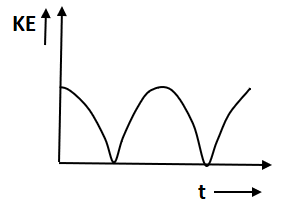
B.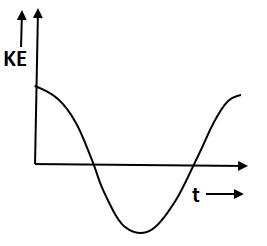
C.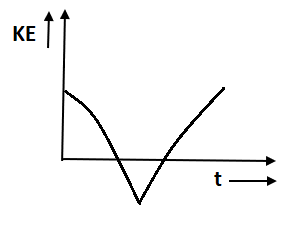
D.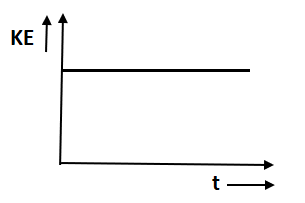

Answer 1

Hint: In a simple harmonic motion (SHM) the distance of positive extreme position and negative extreme position from the mean position is represented as an amplitude(A). At extreme position velocity will be maximum and thus kinetic energy (KE) will also be maximum. By using this we can draw a graph between kinetic energy (KE) and time (t).

Formula used:
The kinetic energy (KE) of a body is given as,
\[KE = \dfrac{1}{2}m{v^2}\]
Where m is the mass and v is the velocity.
simple harmonic motion (SHM), the velocity is given as,
\[v = A\omega \cos (\omega t + \phi )\]
Where A is the amplitude, \[\omega \] is the angular frequency, t is the time taken and \[\phi \] is the phase constant.

Complete step by step solution:
As we know that the kinetic energy (KE) of a body is,
\[KE = \dfrac{1}{2}m{v^2}\]
 For a body performing simple harmonic motion (SHM), the velocity is given as.
\[v = A\omega \cos (\omega t + \phi )\]
Therefore, we have;
\[KE = \dfrac{1}{2}m{A^2}{\omega ^2}{\cos ^2}(\omega t + \phi )\]

This gives kinetic energy that will always be positive. Thus, option B and C which represent negative kinetic energy violate the condition so cannot be the answer. Option D which represents constant kinetic energy also violates the condition. Option A represents the positive kinetic energy.

Hence option A is the correct answer.

Note: The kinetic energy is defined as the energy which is possessed by a body when it is in the state of motion. The energy in the simple harmonic motion (SHM) is shared between elastic potential energy (PE) and kinetic energy (KE). The energy of a particle oscillating in SHM depends on the mass of the particle, frequency and amplitude of oscillation.