Question

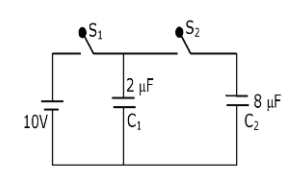
A 2μF capacitor $C_1$ is first charged to a potential difference of 10V using a battery. Then the battery is removed and the capacitor is connected to an uncharged capacitor $C_2$ of 8 μF. The charge in $C_2$ on equilibrium condition is ________ μC. (Round off to the Nearest Integer)

Answer 1

Hint: Capacitors are those devices which are used to store the chemical energy and provide instantaneous energy to the circuit. Capacitance is the ability of a capacitor to store that energy. It can be calculated as C = Q/V , where Q is the charge on the positive plate of the capacitor and V is the potential difference. Capacitance is positive and scalar and it does not depend on charge and potential difference.

Complete answer:
To solve the above question, we first need to find the equilibrium state of the circuit.
1. When $C_{1}$ is fully charged then the charge on $C_{1}$ will be:-
$Q = C_{1} \times V = 2 \times 10 = 20 \mu C$
2. When the battery is removed and the capacitor is connected then,

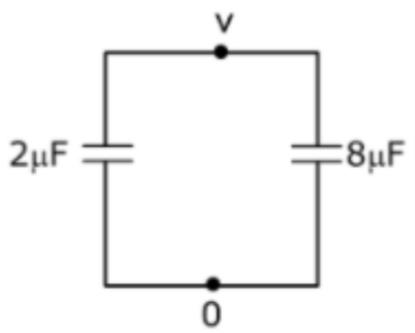
this is the state of equilibrium.

Now, in order to find charge on $C_{2}$, we first need to find voltage on $C_{2}$ which can be calculated as follows:-
$\left(C_{1} V\right) + \left(C_{2} V\right) = Q$
$\left(2 \times V\right) + \left(8 \times V\right) = 20 $
$10 \times V = 20 $
$V = 2~Volt$

Now,
$Q = C_{2}\times V$
$Q = 8 \times 2 $
$Q = 16 \mu C$

Hence, the correct answer is $16 \mu C$.

Note: For practical purposes, the unit farad is quite large. Even a massive body like the earth has a capacitance of $710 \mu F$. A capacitor is a device that retains electrical charges and generates power when needed. Depending on the usage of capacitor, the value of capacitance can either be fixed or variable. Although from the equation it may seem that capacitance depends on charge and potential, it actually depends on size and area of the capacitor used.