JEE Advanced 2024 Thermodynamics Notes

• System: A "system" is any area of the universe that is regarded as "separate''.

• Surroundings: System-interacting component of the universe that is separate from it.

• Boundary: Anything that separates the system from its surroundings.

• Open: If there is an exchange of matter and energy with the environment.

• Closed: If there is an exchange of energy but no exchange of matter.

• Isolated: If there is no exchange of matter and energy.

• Thermodynamic parameter: The variables which describe the state of matter, e.g. pressure, volume, temperature.

• Thermodynamic equilibrium: The system is said to be in equilibrium if the variable remains constant over time.

Intensive Properties

Temperature, pressure, density, concentration, and other system properties that do not depend on the system's mass.

Extensive Properties

Volume, energy, enthalpy, entropy, and other properties of a system that depend on its mass.

State Functions

System property that is determined solely by the system's state rather than the path. For instance, pressure, volume, temperature, internal energy, enthalpy, entropy, and so on.

• Heat: According to thermodynamics, heat is energy that is transferred into or out of a system through means other than work done by the system or the movement of matter.

• Internal energy: The system's kinetic energy and potential energy are added together to form internal energy. When a reaction is operated at constant pressure, the change in internal energy (ΔU)of a reaction is equal to the heat acquired or lost (enthalpy change) in a reaction.

• Work: According to thermodynamics, a system performs work when it transfers energy to its surroundings by a mechanism that allows the system to spontaneously exert macroscopic forces on those surroundings. Through appropriate passive links, the work can, for instance, lift a weight in the environment.

Enthalpy

• The heat absorbed or released during a process at constant pressure is equal to the Enthalpy change. Enthalpy is also known as "heat content," but because it is an interesting and unusual word, most people prefer to use it. 

• Entropy is derived from the Greek word for "turning," and enthalpy is derived from the Greek word for "warming." Entropy is usually stressed on the first syllable, while enthalpy is usually stressed on the second. 

$\mathrm{H}=\mathrm{U}+\mathrm{PV}$

At constant pressure: $dH=dU+pdV$

• For system involving mechanical work only:

$d H=Q_{\mathrm{p}}$ (At constant pressure)

Here, $\mathrm{H}=$ Enthalpy of the system

$\mathrm{U}=$ Internal energy of the system

$p$ = Pressure of the system

$V=$ Volume of the system

• For exothermic reactions: dH is negative

• For endothermic reactions: dH is positive

Zeroth Law of Thermodynamics

• If two bodies A and B are in thermal equilibrium with a third body C separately, then bodies A and B will be in thermal equilibrium with one another.

Triple Point of Water

• The triple point of water is defined as the pressure and temperature at which water coexists in equilibrium in all three states of matter, namely ice, water, and vapour.

• The triple point of pure water is at 0.01°C (273.16K, 32.01°F) and 4.58 mm (611.2Pa) of mercury and is used to calibrate thermometers.

First law of Thermodynamics

• If $\Delta \mathrm{Q}$ is heat given to the system and $\Delta \mathrm{W}$ is work done by the system, then $\Delta \mathrm{U}$ (the change in internal energy) can be written as: $\Delta U=\Delta Q-\Delta W$

• This is the law of conservation of energy. It can be stated in differential form, $d Q-d W=d U$and in time rate form: $\dfrac{d Q}{d t}-\dfrac{d W}{d t}=\dfrac{d U}{d t}$

• Heat supplied to the system is considered positive, while heat rejected by the system is considered negative.

• Work performed by the system is positive, while work performed on the system is negative.

• The change in internal energy is determined by the system's initial and final states $\Delta U=n_{v} \Delta T$ for all processes.

Second Law of Thermodynamics

• Clausius statement: Without the help of an outside agency, heat cannot move from a cold body to a hot body.

• The Kelvin-Planck statement: It is impossible for any device that runs in a cycle to accept heat from a single reservoir and create a net quantity of work, according to the Kelvin-Planck principle.

Third Law of Thermodynamics

• Any crystalline solid entropy decreases as the temperature approaches absolute zero. It's because a crystal at absolute zero has complete order.

• Since many substances do not have zero entropy at absolute zero, this law has a constraint.

• For instance, a substance that is glassy and contains a variety of isotopes.

Entropy

• The quantity of energy that cannot be used to perform work is measured by an object's entropy. The number of alternative arrangements that the atoms in a system can have is also measured by entropy. Entropy is a measure of uncertainty or unpredictability in this sense.

Entropy Formula

• Entropy can also be calculated using a variety of equations, including:

• Entropy will be zero if the process is occurring at a constant temperature.

$\Delta S_{\text {system }}=\dfrac{q_{\text {rev }}}{T}$

Here $\Delta S=$ is the change in entropy

$q_{\text {rev }}=$ refers to the reverse of heat

$\mathrm{T}=$ refers to the temperature in Kelvin

Joule's Law

• It asserts that a thermodynamic system's output of work is directly proportional to the amount of heat.

$W \propto Q$

$W=J Q$

Here $\mathrm{J}$ is called the mechanical equivalent of heat and it is equal to $4.184 \mathrm{~J} / \mathrm{cal}$.

Work Done

• The work done by the gas (or system) on the environment can be calculated as $\mathrm{dW}=\mathrm{PdV}$

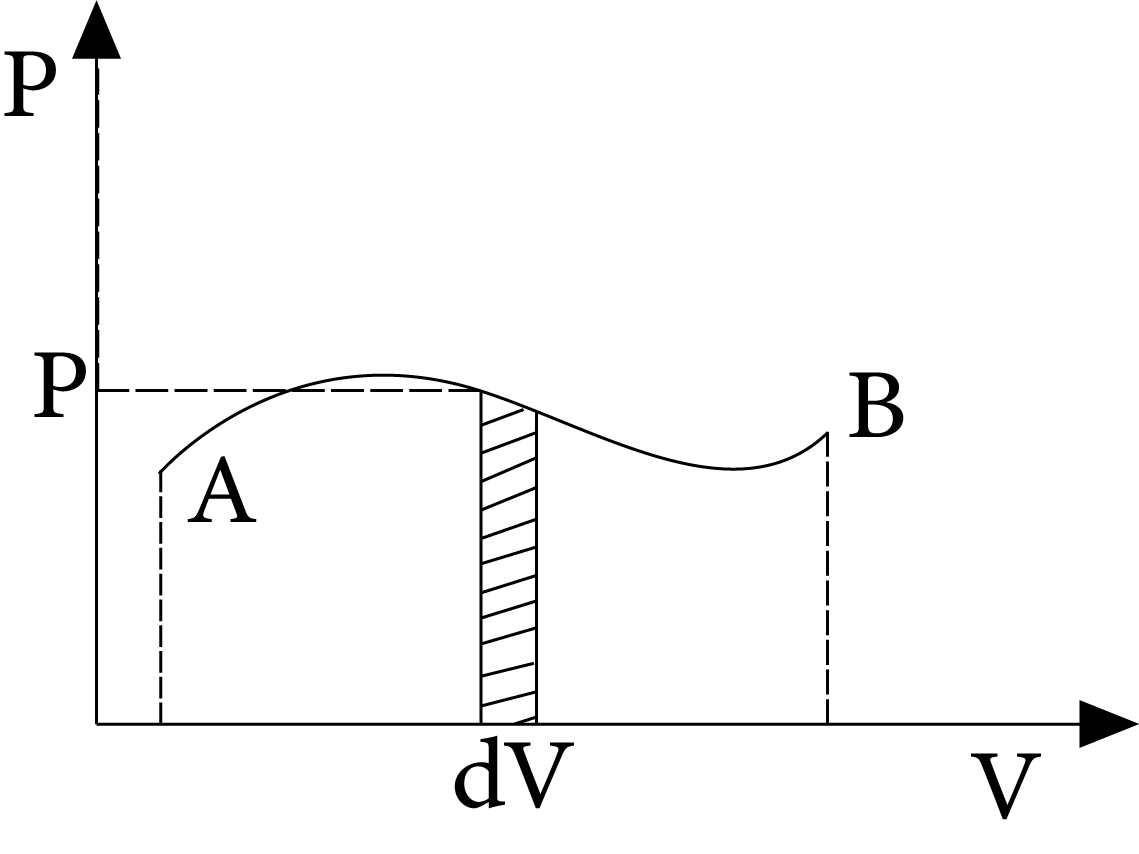
Work Done

• $\therefore W=\int_{{{V}_{i}}}^{{{v}_{f}}}{P}dV$

Here, elemental work is accomplished by the system's pressure during an elemental change in volume (dV). The area under the curve A B and the V-axis is equal to the work completed in the process A B.

Thermodynamic processes 

Isobaric Process

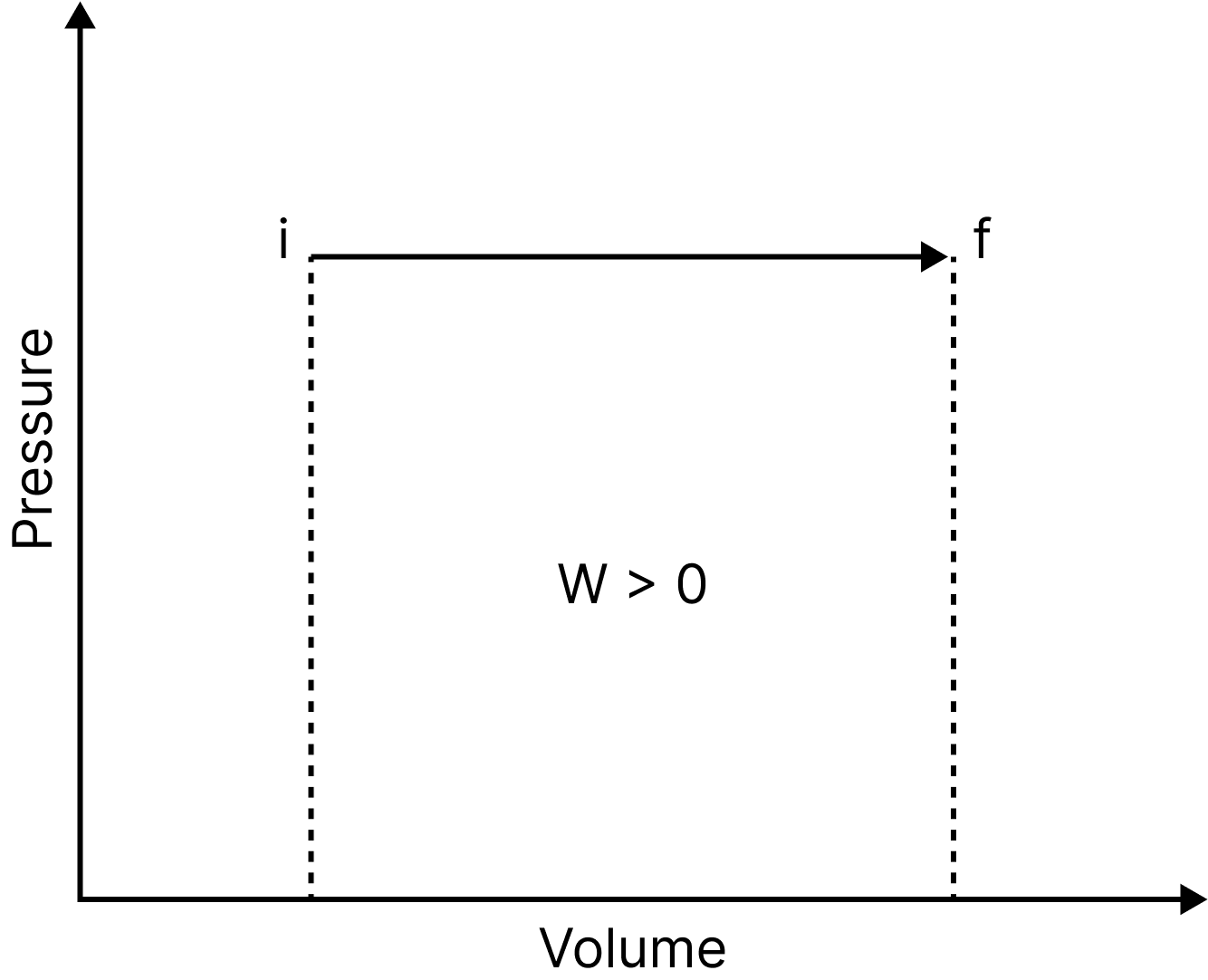
Pressure Volume Graph

• An isobaric process is one that occurs at a constant pressure. Isobaric processes include, for instance, boiling water to steam in an open saucepan or freezing water to ice at a constant atmospheric pressure. In this process, the work done is equal to $\mathrm{P} \Delta \mathrm{V}$.

Isochoric Process

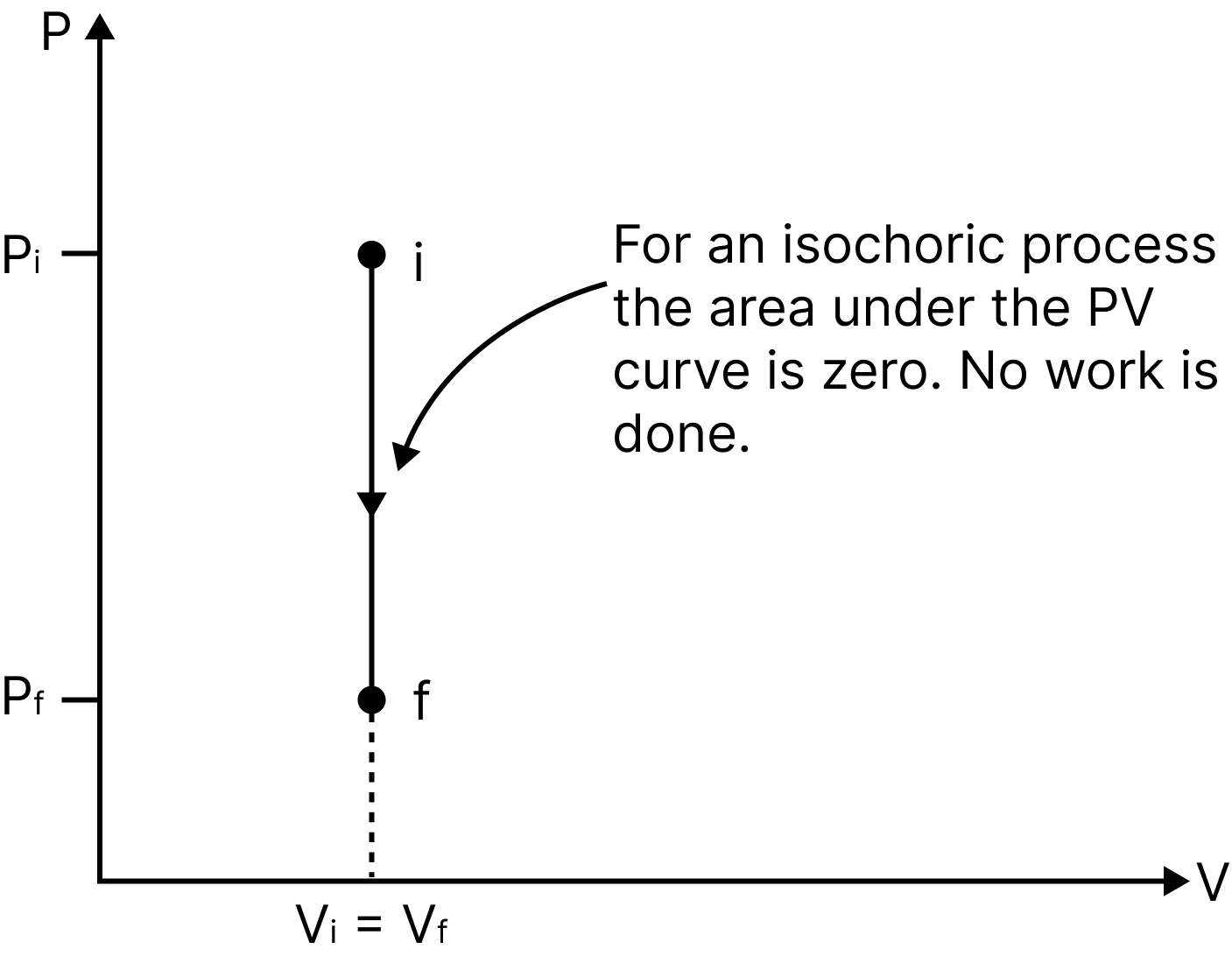
Isochoric Process

• A process taking place at constant volume $(\Delta V=0)$ is called an isochoric process.

• Work done, $d W=P \cdot d V=0$

Thus, net change in internal energy, $\Delta U=\Delta Q$

Adiabatic Process

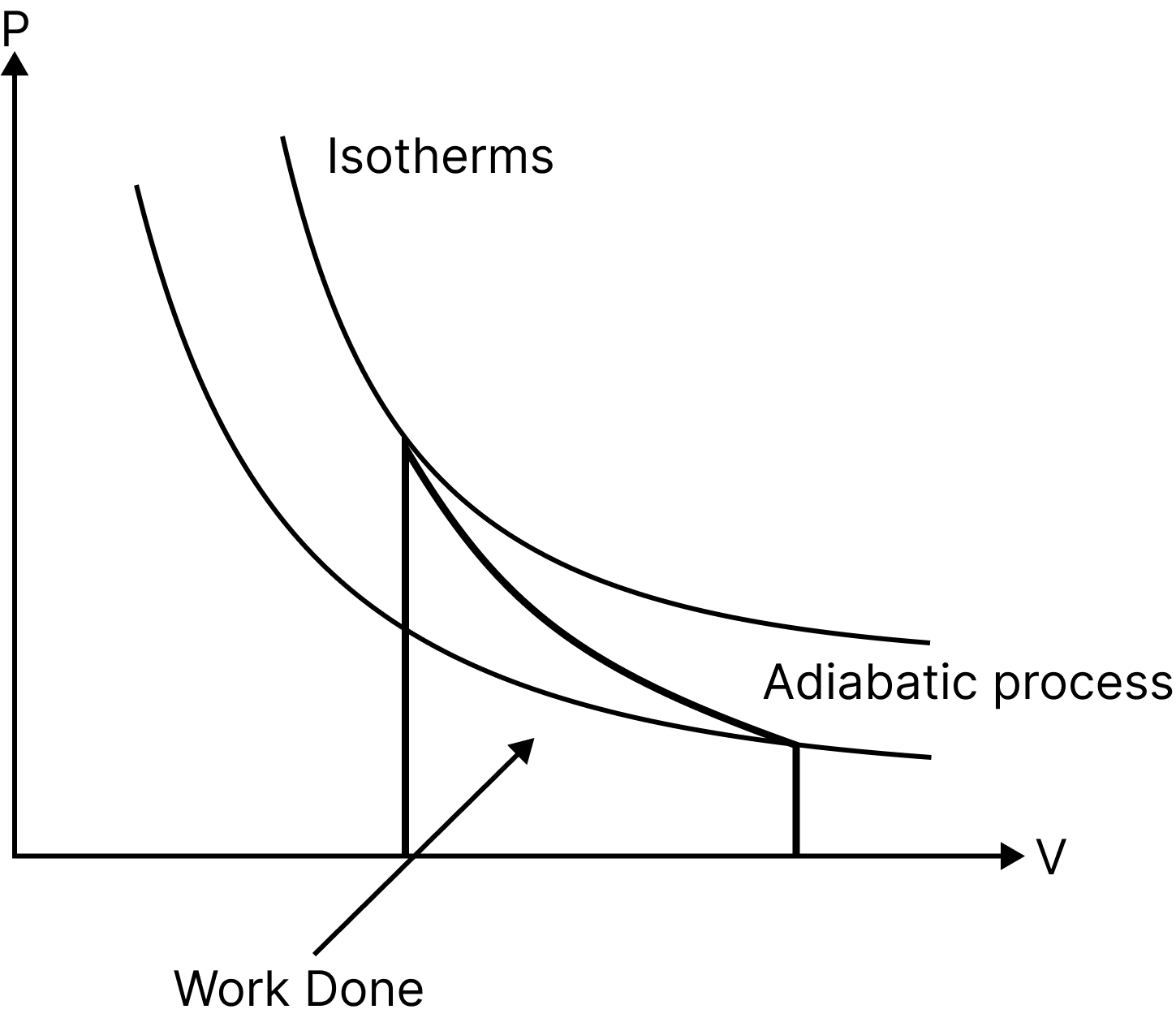
Adiabatic Process

• A process is referred to as adiabatic when a system transitions from an initial state to a final state without any heat flowing into or out of the system.

• Such a process can take place when the system is thermally isolated from its environment or when it moves so quickly that there is little to no opportunity for heat to enter or leave the system.

Such as heat supplied, $Q=0$

• Thus, net change in internal energy, $\Delta \mathrm{U}=-\Delta \mathrm{W}$

i.e. In an adiabatic process, the system accomplishes function at the expense of its own internal energy.

• For an adiabatic process, $d Q=0$

$\Rightarrow d U+P d V=0$…………….(1)

• For an ideal gas, $d U=n C_{v} d T$………….(2)

Similarly, $P V=n R T \Rightarrow d T=\dfrac{P d V+V d P}{n R}$    $\ldots(3)$

Equations (2) and (3) are substituted in equation (1)

$n C_{v}\left(\dfrac{P d V+V d P}{n R}\right)+P d V=0$

$\Rightarrow \quad\left(\dfrac{C_{v}}{R}+1\right) P d V+\dfrac{C_{v}}{R} V d P=0$

$\Rightarrow C_{p} P d V+C_{v} V d P=0 \Rightarrow \dfrac{C_{p}}{C_{v}}\left(\dfrac{d V}{V}\right)+\dfrac{d P}{P}=0$

$\Rightarrow \gamma \ln \text{V}+\ln \text{P}=\ln \text{K}$ 

$\Rightarrow P V^{\gamma}=K$ (Constant)

When an ideal gas expands adiabatically from initial volume $V_{i}$ to final volume ${{V}_{f}}$, then work done

$W=\int_{{{V}_{i}}}^{{{V}_{f}}}{P}dV$

As, $P{{V}^{\gamma }}=K\text{ (constant) } $

$\therefore W=K\int_{{{V}_{i}}}^{{{V}_{f}}}{{{V}^{-\gamma }}}dV=K\left[ \dfrac{{{V}^{-\gamma +1}}}{-\gamma +1} \right]_{{{V}_{i}}}^{{{V}_{f}}}=\dfrac{1}{\gamma -1}\left[ \dfrac{K}{V_{i}^{\gamma -1}}-\dfrac{K}{V_{f}^{\gamma -1}} \right]=\dfrac{1}{\gamma -1}\left[ \dfrac{{{P}_{i}}V_{i}^{\gamma }}{V_{i}^{\gamma -1}}-\dfrac{{{P}_{f}}V_{f}^{\gamma }}{V_{f}^{\gamma -1}} \right] $

$ W=\dfrac{{{P}_{i}}{{V}_{i}}-{{P}_{f}}{{V}_{f}}}{\gamma -1} $

Since $P_{i} V_{i}=n R T_{i}$ and ${{P}_{f}}{{V}_{f}}=nR{{T}_{f}}$

$\therefore W=\dfrac{nR\left( {{T}_{i}}-{{T}_{f}} \right)}{\gamma -1}$

Adiabatic Relations

(i) $P{{V}^{\gamma }}=$ Constant 

$\Rightarrow {{\text{P}}_{\text{i}}}\text{V}_{i}^{\gamma }={{\text{P}}_{\text{f}}}{{\text{V}}_{f}}$

(ii) $P{{V}^{\gamma }}=$ Constant

As $P=\dfrac{nRT}{v}$

$\therefore \quad (nRT/V){{V}^{\gamma }}=$ Constant

Or $T{{V}^{\gamma -1}}$= constant$\Rightarrow {{T}_{i}}V_{i}^{\gamma -1}={{T}_{f}}V_{f}^{\gamma -1}$

(iii) $P{{V}^{\gamma }}=$ Constant

$\text{ As }V=\dfrac{nRT}{P}\quad \Rightarrow P{{\left( \dfrac{nRT}{P} \right)}^{\gamma }}=\text{ constant }$

$\text{ or }{{T}^{\gamma }}{{P}^{1-\gamma }}=\text{ constant }$

$\Rightarrow T_{i}^{\gamma }P_{i}^{1-\gamma }=T_{f}^{\gamma }P_{f}^{1-\gamma }$

Isothermal Process

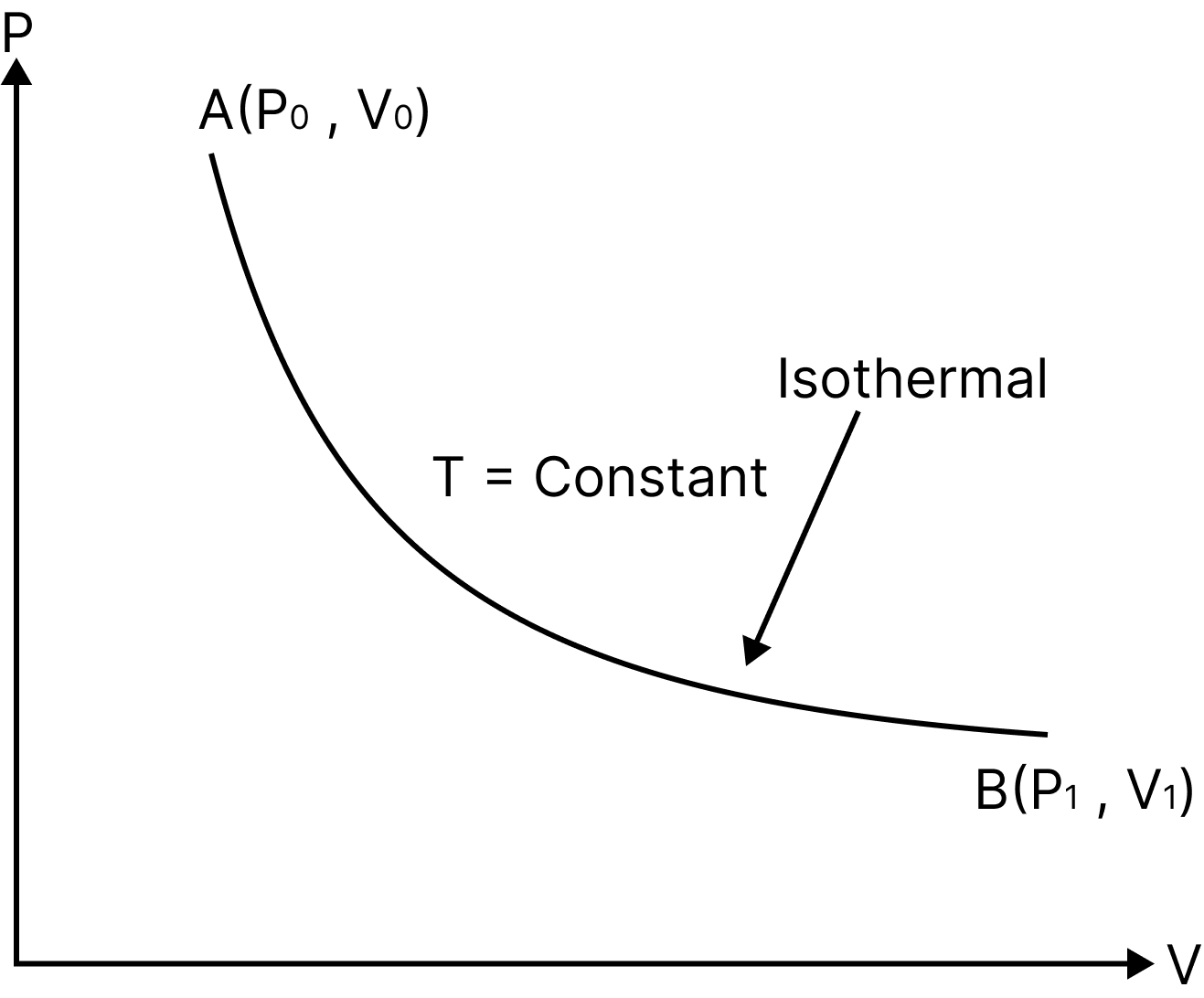
P-V Diagram

• An "isothermal" process is one that takes place in a system while ensuring that its temperature stays constant.

• Such a process is possible if the system is enclosed in a chamber with perfect conductivity and is carried out extremely slowly to allow for adequate time for heat exchange.

• For instance the temperature of the system remains constant $(T=$ constant), thus $P V=$ constant.

The internal energy of an ideal gas only varies with temperature.$\mathrm{dU}=0 \Rightarrow \mathrm{dQ}=\mathrm{dW} .$

• When an ideal gas expands from initial volume $V_{i}$ to final volume ${{V}_{f}}$ at constant temperature, the work done

$W=\int_{{{V}_{i}}}^{{{V}_{f}}}{P}dV$

As $P V=n R T$

$\therefore \quad W\text{ }=nRT\int_{{{V}_{i}}}^{{{V}_{\text{f}}}}{\dfrac{dV}{V}}$

$W =n R T \ln \left(\dfrac{V_{f}}{V_{i}}\right) ; \quad W=n R T \ln \left(\dfrac{P_{i}}{P_{f}}\right)$

Free Expansion

• Free expansion refers to the process when a gas expands in the absence of any external pressure (vacuum). Free expansions are like adiabatic processes with no work done because there is no work done on or by the system and the process moves very quickly due to which no heat is introduced into or removed from the system.

• Consider a rigid-walled adiabatic vessel that is separated into two halves, one of which is filled with a gas and the other of which is evacuated. The gas rushes into the vacuum and expands without restriction when the partition is suddenly broken.

Free Expansion

Consequently, net change in internal energy

As, 

${{U}_{f}}-{{U}_{i}}=Q-W$

${{U}_{i}}={{U}_{f}}$

In free expansion, the initial and final internal energy are equal.

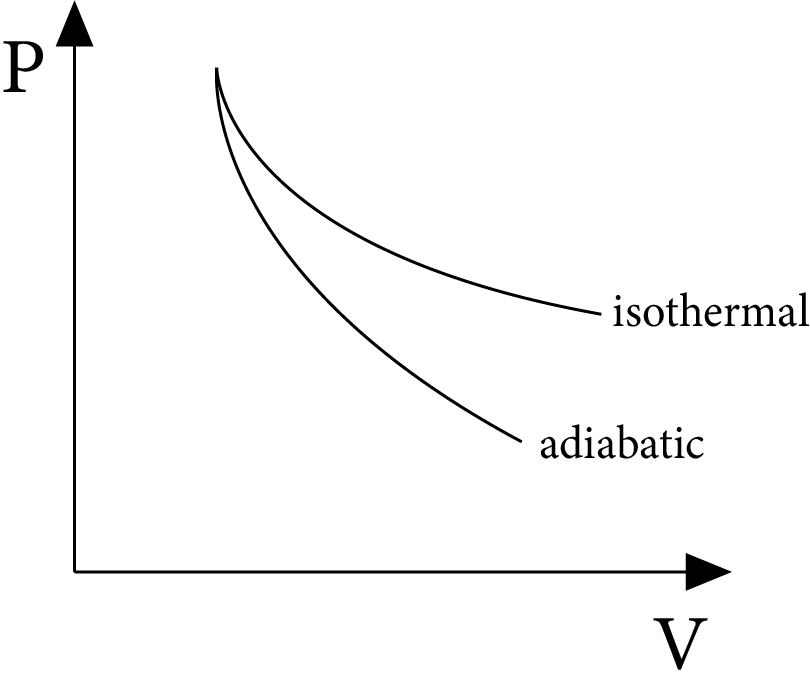
Slope of Isothermal and Adiabatic Processes

• For an isothermal process:

$P V=$ Constant

Differentiating, $P d V+V d P=0$

or ${{\left( \dfrac{dP}{dV} \right)}_{\text{isothermal }}}=-\dfrac{P}{V}$

• For an adiabatic process:

\[P{{V}^{\gamma }}\]= constant

Differentiating

$Pd{{V}^{\gamma -1}}dV+{{V}^{\gamma }}dP=0$ 

or ${{\left( \dfrac{dP}{dV} \right)}_{\text{adiabatic }}}=\quad -\gamma \,\dfrac{P}{V}$

For a given pressure and volume, the adiabatic curve's slope is $\gamma$ times that of the isothermal curve, and both slopes are negative.

Reversible and Irreversible Process:

• Any process which returns to its initial state of thermodynamic variables at each stage of variation as it proceeds in a direct process is called a reversible process. A complete reversible process is an ideal concept as it can never be realised in practice because dissipative forces cannot be completely eliminated.

• A process is called irreversible if it cannot be retracted back exactly in the opposite direction. During an irreversible process, work is always done to overcome friction or other non-conservative forces. Energy is also dissipated. Most of the processes occurring in nature are irreversible.

Cyclic Process 

• A cyclic process is a collection of processes that a certain system goes through such that the initial and final states are the same.

$\Delta U=0$ for a cyclic process.

Since $\Delta U=Q-W$

$\therefore 0=Q-W \quad \text { or } \quad Q=W$

Efficiency of a Cyclic Process

• The ratio of work completed to heat supplied is known as a cycle's efficiency. Efficiency of a cycle $=\dfrac{\text { work done }}{\text { heat supplied }}$.

• Consider an ideal gas going through the cycle as shown in figure. If $Q_{1}$ and $Q_{2}$ be the heat supplied, while $Q_{3}$ is the heat rejected in the process, then

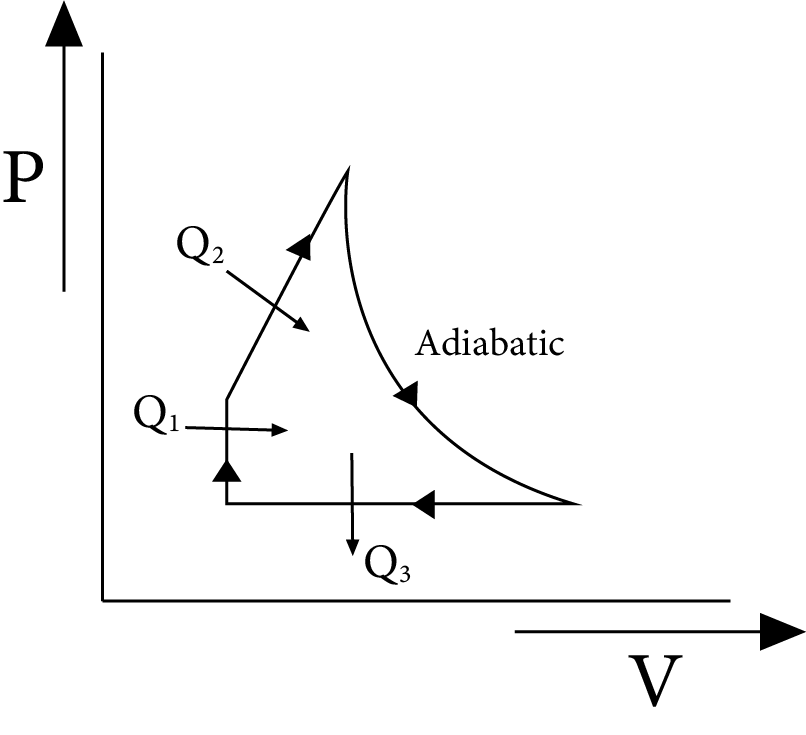
Efficiency of a Cyclic Process

$\text{ Efficiency }=\dfrac{\text{ work done }}{\text{ heat supplied }}$

$=\dfrac{\left(Q_{1}+Q_{2}\right)-Q_{3}}{\left(Q_{1}+Q_{2}\right)}=1-\dfrac{Q_{3}}{Q_{1}+Q_{2}}$

Carnot Engine Principles

Carnot Engine

• The efficacy of an irreversible heat engine is always lower than the efficiency of a reversible one operating between the same two reservoirs, according to Carnot principles, which are only applicable to cyclical devices like heat engines.

• Every reversible heat engine that operates between the same two reservoirs performs equally well.

• The temperature of the combustion room must rise in order to improve the thermal efficiency of a gas power turbine. For instance, the high-temperature gas cannot be supported by turbine blades, which will eventually cause early fatigue.

Carnot’s Theorem

• According to this theorem, no engine operating between two known temperatures can be more efficient than a reversible engine operating between similar two temperatures, and all reversible engines operating between the same two temperatures have the same efficiency, regardless of the type of working material. 

• The reversible engine will always be more productive than the irreversible one, according to the Carnot theorem. The reversible heat engine functions as a heat pump and runs on a reverse cycle.

The Efficiency of Carnot’s Cycle

• The Carnot cycle, which denotes the maximum efficiency possible for an engine cycle, is reversible. Since practical engine cycles cannot be reversed, they are essentially significantly less efficient than Carnot cycles when operating at comparable temperatures. 

• The addition and withdrawal of the working fluid during the cycle are two aspects that affect efficiency. Maximum effectiveness of the Carnot cycle,

$\eta=W / Q_{1}=\left[Q_{1}-Q_{2}\right] / Q_{1}=1-\left[Q_{2} / Q_{1}\right]=1-T_{2} / T_{1}$

Refrigerator

• Refrigerators function by converting the refrigerant circulating inside them from a liquid to a gas. 

• This process, known as evaporation, cools the surrounding environment and achieves the desired effect. You can try this process for yourself by putting a drop or two of alcohol on your skin.

Refrigerator Working b/w Source & Sink

Coefficient of Performance

A heat pump, refrigerator, or air conditioning system's coefficient of performance, or COP, is a ratio of useful heating or cooling provided to work required. Higher COPs imply lower operating costs.

The coefficient of performance for heating is given by the equation:

$K_{\text {heating }}=\dfrac{Q_{H}}{W_{\text {in }}}$

Here:

$Q_{H}$ is the heat delivered by the heat pump

$W_{i n}$ is the work input to the system

$K_{\text {heating }}$ is the heating coefficient of performance.

Heat Capacity

• If a quantity $\Delta Q$ of heat raises the temperature of a body through $\Delta T$, then heat capacity is given by

$H=\dfrac{\Delta Q}{\Delta T} J / K$

• A body's heat capacity is the amount of heat necessary to raise its temperature by one degree Celsius.

Specific Heat

• The situation is the heat required to raise the temperature by $1^{\circ} \mathrm{C}$ or $1^{\circ} \mathrm{K}$ for a unit mass of the body.

$\mathrm{C}=\dfrac{\Delta \mathrm{Q}}{\mathrm{m} \Delta \mathrm{T}}$

• In heat and thermodynamics problems, we normally work with ideal gases and need molar specific heat.

• Therefore, molar heat capacity, $\mathrm{C}=\dfrac{\Delta \mathrm{Q}}{\mathrm{n} \Delta \mathrm{T}}$, wherever $\mathrm{n}=$ number of moles.

In differential form, $C=\dfrac{1}{n}\left(\dfrac{d Q}{d T}\right)=\dfrac{1}{n}\left(\dfrac{d U}{d T}\right)+\dfrac{1}{n}\left(\dfrac{d W}{d T}\right)$

• Because dw varies with the procedure, so does the molar heat capacity.

When heat $\Delta Q$ is given to a gas of mass $m$; (keeping its volume constant) and the temperature rises by $\Delta T$, then the heat capacity at constant volume is expressed as

$C_{V}=\left(\dfrac{\Delta Q}{n \Delta T}\right)_{\Delta V=0}=\dfrac{1}{n} \dfrac{d U}{d T}$

• When the pressure of a gas of mass $m$ is kept constant and heat $\Delta Q$ is given to it, and temperature rises by$\Delta T$, then molar heat capacity at constant pressure is expressed as

$C_{P}=\left(\dfrac{\Delta Q}{n \cdot \Delta T}\right)_{\Delta P=0}=\dfrac{1}{n} \dfrac{d U}{d T}+\dfrac{1}{n} P \dfrac{d V}{d T}=C_{v}+R$

Relation between $C_{p}$ and $C_{v}$ is, $C_{p}-C_{v}=R$

Principle of Calorimetry:

• Heat passes from the hot object to the cold object when two things of different temperatures come into touch. 

• Heat lost by the hot object = heat acquired by the cool object if the system is sufficiently thermally separated from its surroundings.

Latent Heat (L):

• The amount of heat absorbed or released by a body of unit mass during a change of condition while its temperature remains constant is referred to as latent heat.

• Heat absorbed or emitted during a state change,

$\mathrm{Q}=\mathrm{mL}$, 

Here $\mathrm{m}$ is mass of the body and $\mathrm{L}$ is latent heat.

$L=Q / m$

Important Formula

Example 1: The figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuously from 0 to 500 K at a constant rate. Ignoring any volume change, the following statement(s) is(are) correct to a reasonable approximation.

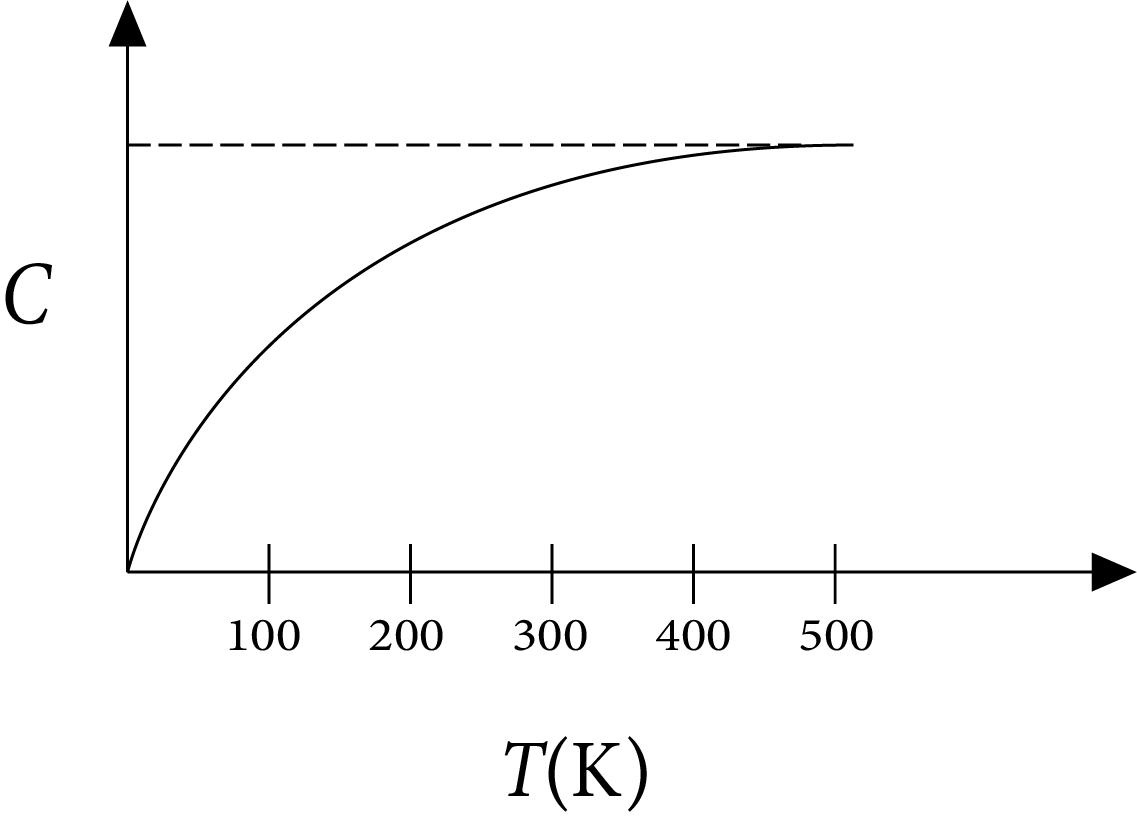
Specific Heat Capacity (C) of a Solid as a Function of Temperature (T)

1. The rate at which heat is absorbed in the range $0-100 \mathrm{~K}$ varies linearly with temperature $\mathrm{T}$.

2. Heat absorbed in increasing the temperature from 0-100 $K$ is less than the heat required for increasing the temperature from $400-500 \mathrm{~K}$.

3. There is no change in the rate of heat absorption in the range $400-500 \mathrm{~K}$.

4. The rate of heat absorption increases in the range $200-300 \mathrm{~K}$.

Ans: A,B,C,D

Sol:

According to definition of specific heat capacity,

$C=\dfrac{\Delta Q}{m \Delta T}$

$\Rightarrow \Delta Q=m C \Delta T \therefore \dfrac{\Delta Q}{\Delta t}=m C \dfrac{\Delta T}{\Delta t}$

Rate of heat absorbed $R=\dfrac{\Delta Q}{\Delta t}$

$\Rightarrow \dfrac{\Delta Q}{\Delta t} \propto C$

(a) $\ln 0-100 \mathrm{~K}$,

C increases with $\mathrm{T}$ but not linearly. So $\mathrm{R}$ increases but not linearly.

(b) As $\Delta Q=m C \Delta T$

$Q=m \int C \Delta T$

$=\mathrm{m}$ area under C-T curve

From the graph it is clear that area under C-T is more in 400-500 $\mathrm{K}$ than in $0-100 \mathrm{~K}$.

Therefore, heat absorbed in $0-100 \mathrm{~K}$ is less than in $400-500 \mathrm{~K}$.

(c) $\ln 400-500 \mathrm{~K}$

$\mathrm{C}$ remains constant so there is no change in $\mathrm{R}$.

(d) $\ln 200-300 \mathrm{~K}$

$\mathrm{C}$ increases so $\mathrm{R}$ increases.

Example 2: A reversible engine has an efficiency of $\dfrac{1}{4}$. If the temperature of the sink is reduced by $58^{\circ} \mathrm{C}$, its efficiency becomes double. Calculate the temperature of the sink:

1. $174^{\circ} \mathrm{C}$

2. $280^{\circ} \mathrm{C}$

3. $180.4^{\circ} \mathrm{C}$

4. $382^{\circ} \mathrm{C}$

Answer: A

Complete solution:

We know that formula of efficiency $\eta=1-\dfrac{T_{2}}{T_{1}}$

Putting values in above equation we get$\dfrac{1}{4}=1-\dfrac{T_{2}}{T_{1}}$

$\dfrac{T_{2}}{T_{1}}=\dfrac{3}{4} \ldots(\mathrm{i})$

$\dfrac{1}{2}=1-\dfrac{T_{2}-58}{T_{1}}$

$\dfrac{T_{2}}{T_{1}}=\dfrac{58}{T_{1}}=\dfrac{1}{2}$

$\dfrac{3}{4}=\dfrac{58}{T_{1}}+\dfrac{1}{2}$

$\dfrac{1}{4}=\dfrac{58}{T_{1}} \Rightarrow T_{1}=232$

$T_{2}=\dfrac{3}{4} \times 232$

$T_{2}=174 \mathrm{~K}$

Hence, the temperature of the sink is $T_{2}=174 \mathrm{~K}$.

Common Errors or Mistakes That Should be Avoided by the Students Keeping the Exam Point of View:

• Forgetting that there’s something called latent heat in thermodynamics.

• Students forget to write the working formula and not read definitions properly.

• Students also write improper units without checking their compatibility.

• Calculation errors when doing problems

• The answers should be in accordance with the marks allotted. For example, a question of 2 marks should not be answered in a whole page. Students should stick to the important points to gain full marks in the question. This will also help to have sufficient time to complete the paper.

• Sometimes, even good students forget to write down the formula when working on numerical. Students should note that few marks are allotted for the formula and this will result in not scoring the full mark for the numerical.

• Students should learn the formula thoroughly to avoid confusion in the examination. Often students get confused and flip the numerator and denominator in the formulae. This results in the entire numerical to be incorrect and no marks are awarded for the answer.

• For diagram questions, it is a must that students label the diagram. To make the paper more presentable, students should mark these labels in a pencil or with a different colour pen.

• 1 mark questions that ask for “Yes” or “No” answers should be written along with its reason to achieve full marks in this question. ½ mark is allotted for each part.

• In the exam, most of the questions have parts in it. Each part is allotted a specific mark and often students overlook these small parts asked and results in losing marks in the question either ½ a mark or 3 marks for the same.

• Students should avoid making question mistakes for the answer they are writing. Marks will not be allotted for incorrect question numbers.

• When a student wants to rewrite a certain question that has already been answered, they must make sure that the incorrect answer is struck out. If a student fails to strike out the incorrect answer, as per the CBSE guidelines, the examiner will take the first attempt as the answer to the question and ignore the second.

Importance of Physics Thermodynamics

The behaviour of heart energy in a system can be measured by using the concept of thermodynamics. This chapter explains how the changes in energy occur due to work done in a system. The ideal conditions to measure the internal energy, work done, and heat will be explained in different systems.

The chapter describes the different types of systems with proper definitions and mathematical expressions. Students will learn to differentiate and identify the common systems such as open systems, closed systems, and isolated systems. This chapter will also explain state variables and state functions. The correlation of the state variables such as temperature, surface area, volume, pressure, and mass with the state functions such as internal energy, entropy, enthalpy, etc will be explained in detail.

The laws of thermodynamics will be explained elaborately. Students will learn how these laws have been framed and what conditions have been considered to derive their mathematical expressions. These laws enable us to define the energy state of a system and changes in energy level due to work done.

This chapter is of utmost importance as it explains how the internal energy, heat, and work done are interrelated to each other. to make it easier, you can refer to the Thermodynamics notes prepared by the subject experts.

Benefits of Vedantu’s Thermodynamics Revision Notes

• The main objective of developing these notes is to offer a concise format of the entire chapter in a few pages. You will find it very easy to revise this chapter within a short span of time.

• Students can download these notes for free and can refer to them at their convenience. Using these notes to prepare and revise this chapter according to your study schedule will become much easier.

• You can resolve doubts based on this chapter on your own by using the revision notes and proceed to completely learn it.

• The precise format of these notes will also help you to memorise the definitions, formulas, principles, and mathematical expressions of the chapter terminologies easily. With the help of an easier description of the important terms, you can easily recall and answer fundamental questions during the exam.

Download Thermodynamics Notes PDF

Preparing and revising this chapter has never been easier for you. You can now download the PDF version of Thermodynamics Class 11 Physics JEE Advanced notes for free and complete your study material for this chapter. Add these benefits to your study sessions and become more confident in solving the fundamental problems of thermodynamics in the JEE Advanced exam.

Important Related Links for JEE Main and JEE Advanced