Introduction to Carnot Theorem
Carnot theorem, often known as Carnot's rule, was created in 1824 by Nicolas Léonard Sadi Carnot and is a theory that describes the greatest efficiency that any heat engine may achieve. A Carnot engine's efficiency is solely determined by the temperatures of its hot and cold reservoirs.
Carnot Theorem
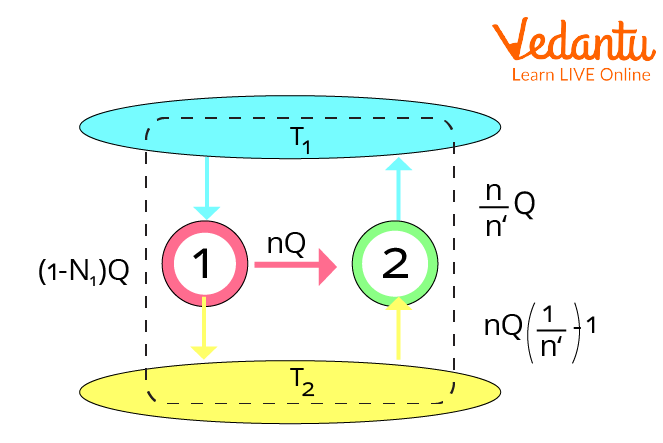
This theorem has the conclusion that every Carnot heat engine operating across two heat reservoirs is equally efficient, irrespective of the working substance or operation details.
History of Nicolas Léonard Sadi Carnot
Carnot's theorem was given in 1824 by Nicolas Léonard Sadi Carnot, a French Army mechanical engineer, military scientist, and physicist known as the "Father of Thermodynamics."
Nicolas Léonard Sadi Carnot (1 June 1796 – 24 August 1832)
The Carnot theorem is a consequence of the second law of thermodynamics. It was historically founded on contemporary caloric theory and predated the formation of the second law.
Carnot Theorem Statement
According to Carnot's theorem, the heat engine's efficiency has no boundaries; it can be as high as it can be dependent on the hot and cold reservoir temperatures.
\[{\eta _{\max }} = {\eta _{carnot}}=1-\dfrac {T_C}{T_H}\]\[\]
Where,
\[T_C\] - Absolute temperature of the cold source
\[T_H\] - Absolute temperature of the hot source
Carnot’s Theorem Proof
Consider a heat engine that draws heat Q1 from a heat reservoir at T1, delivers work W, and dumps heat Q2 into a heat sink at T2.
The heat engine operates in cycles( each of which includes two isothermal and two adiabatic processes), meaning it takes in heat Q1, performs work W, dumps heat Q2, and then returns to its original, unaltered state.
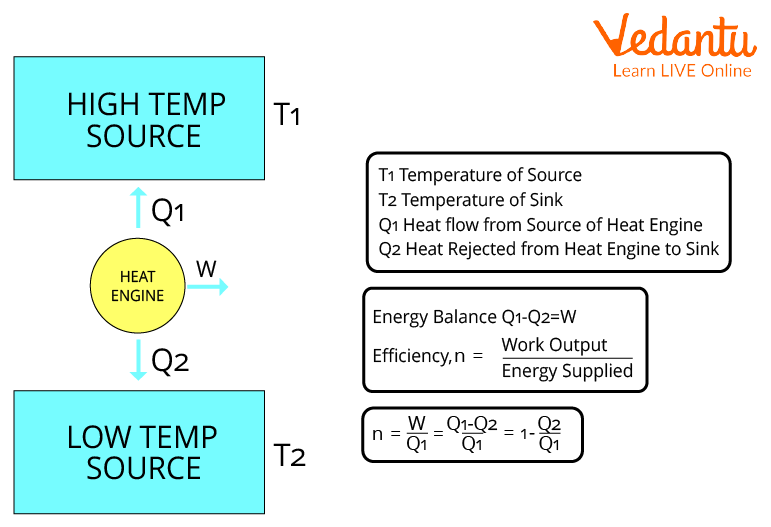
Heat Engine and Efficiency
Consider the universe's net change in entropy \[\Delta S\]\[\].
At a steady temperature T1, the heat reservoir emits heat Q1. As a result, the change in its entropy is:
\[\Delta {S_1} = - \frac{{{Q_1}}}{{{T_1}}}\]
At a steady temperature T2, the heat sink receives heat Q2. As a result, the change in its entropy is:
\[\Delta {S_2} = - \frac{{{Q_2}}}{{{T_2}}}\]
As a result, the universe's net entropy change is,
\[\begin{array}{l}\Delta S = \Delta {S_1} + \Delta {S_2}\\\Delta S = \frac{{{Q_2}}}{{{T_2}}} - \frac{{{Q_1}}}{{{T_1}}}\end{array}\]
Using the second law of thermodynamics, \[\Delta S \ge 0\], it follows that
\[\begin{array}{l}\frac{{{Q_2}}}{{{T_2}}} - \frac{{{Q_1}}}{{{T_1}}} \ge 0\\\frac{{{Q_2}}}{{{T_2}}} \ge \frac{{{Q_1}}}{{{T_1}}}\\\frac{{{Q_2}}}{{{Q_1}}} - \frac{{{T_2}}}{{{T_1}}}\\1 - \frac{{{Q_2}}}{{{Q_1}}} \le 1 - \frac{{{T_2}}}{{{T_1}}}\end{array}\]
Because the left side reflects the efficiency of the supplied heat engine \[\eta\] and the right side indicates the efficiency of a Carnot engine,
\[\eta \le {\eta _{carnot}} \to {\eta _{\max }} = {\eta _{carnot}}\]
Hence proved
Limitations of Carnot Theorem
The Carnot Cycle is an ideal cycle, which means it does not exist and cannot be created. Hence it is only a theoretical concept.
The Carnot Cycle is only used to examine heat engines and does not apply to other sorts of devices.
The output obtained per cycle is quite low.
Carnot Cycle Application
Carnot's theorem is used in engines that turn thermal energy into work.
In a refrigeration system, the Carnot cycle is reversed. We know that a heat engine based on the Carnot engine has the maximum efficiency. Similarly, a change cycle refrigeration system has the highest coefficient of performance.
Solved Examples
1. What is the efficiency of a Carnot engine operating between \[{340^ \circ }C\] and \[{70^ \circ }C\]?
Ans. Given data:
\[\begin{array}{l}{T_1} = {340^ \circ }C = (340 + 273)K\\{T_1} = 613K\\{T_2} = {70^ \circ }C = (70 + 273)K\\{T_2} = 343K\end{array}\]
Carnot's engine efficiency is given by,
\[\begin{array}{l}\eta = 1 - (\frac{{{T_2}}}{{{T_1}}})\\\therefore \,\eta = 1 - (\frac{{343}}{{613}})\\ \Rightarrow \frac{{613 - 343}}{{613}} \approx 0.44\end{array}\]
Therefore, the efficiency of the Carnot engine operating between the given temperatures is about \[44\].
2. A heat engine with a 55% efficiency performs 70kJ of work every Carnot cycle. What amount of heat is rejected in each cycle?
Ans. Given data:
\[\begin{array}{l}\eta = 55\% \\ \Rightarrow \,\eta = 0.55\\w = 70J\end{array}\]
As known,
\[\eta \] = output work/Heat absorbed \[{Q_1}\]
Therefore,
\[\begin{array}{l}0.55 = \frac{{70}}{{{Q_1}}}\\ \Rightarrow {Q_1} = 127.27\end{array}\]
Work = \[{Q_1} - {Q_2}\] (Heat absorbed - Heat rejected)
\[\begin{array}{l}70 = {Q_1} - 127.27\\{Q_1} = 57.27kJ\end{array}\]
So, the amount of heat rejected in each cycle is \[57.27kJ\].
3. Consider Carnot's cycle that produces \[2kJ\] of mechanical work during each cycle and operates between \[{T_1} = 400K\] and \[{T_2} = 560K\]. What is the amount of heat transmitted to the engine by the reservoirs?
Ans. Given data:
\[{T_1} = 400K\]
\[{T_2} = 560K\]
Output Work = \[2kJ\]
Carnot's engine efficiency is given by,
\[\begin{array}{l}\eta = 1 - \frac{{{T_2}}}{{{T_1}}}\\ \Rightarrow \eta = 1 - \frac{{400}}{{560}}\\ \Rightarrow \eta = \frac{{560 - 400}}{{560}}\\ \Rightarrow \eta = 0.28\end{array}\]
Efficiency can also be written as:
\[\eta = \dfrac {\text{output~ work}}{\text{Heat~ supplied}}\]
\[\eta = \dfrac{{2000}}{x}\]
Where ‘x’ is the total heat supplied.
Now substitute the calculated value of efficiency in the above expression.
\[\begin{array}{l}0.28 = \frac{{2000}}{x}\\ \Rightarrow 0.28x = 2000\\ \Rightarrow x = \frac{{2000}}{{0.28}}\\ \Rightarrow x = 7142.85J\end{array}\]
Important Points to Remember
A Carnot cycle employs an ideal gas as a working fluid.
The working substance is subjected to a cyclic operation involving two isothermal and two adiabatic operations in a Carnot cycle.
Important Formulas to Remember from Theorem
The formula for maximum efficiency is as follows:
\[\eta {}_{\max } = 1 - \frac{{{T_2}}}{{{T_1}}}\]
Where \[\eta \] is the efficiency, \[{T_2}\] is the absolute temperature (Kelvins) of the cold reservoir, and \[{T_1}\] is the absolute temperature (Kelvins) of the hot reservoir.
Another formula for efficiency,
\[\eta \] = $\dfrac {\text{output~ work}}{\text{Heat~ supplied}}$
Conclusion
Carnot's theorem illustrates the principle that an irreversible engine's efficiency cannot be greater than that of a reversible engine if both operate between fixed temperature heat reservoirs.
Simple heat engines are less effective and efficient when employed between two heat reservoirs, but Carnot heat engines are more efficient. Regardless of their operation, the Carnot engines are always efficient.
FAQs on Carnot Theorem and Its Applications
1. Why Carnot engine is considered the most efficient engine?
Maximum efficiency is reached for heat engines that go through a cycle of expansion and compression when the expansion produces the most work, and the compression demands the least amount of work.
It is a fundamental concept of thermodynamics that the maximum work output of a system is obtained when the process is carried out reversibly.
Furthermore, all four steps of the Carnot cycle are reversible. Therefore, the sole criteria that appear to be utilized to prove that the Carnot engine is the most effective are that it is reversible.
2. What is the Carnot cycle?
A Carnot cycle is an ideal thermodynamic cycle that limits the efficiency of any classical thermodynamic engine during heat conversion to work. To ensure a continual supply of work, the working substance is exposed to Carnot's cycle of quasi-static operations. The cycle consists of the following steps when acting as a heat engine.
Isothermal Expansion
Adiabatic or Isentropic Expansion
Isothermal Compression
Isentropic Compression
Because a Carnot cycle is reversible, it inherently reflects the best potential performance. However, practical engines are not reversible due to several factors such as friction, heat transmission to the insulating wall, and so on.
3. What are reversible and irreversible engines?
The reversible and Irrversibles engines are discussed below in-depth :
Reversible Heat Engines are engines having the same and equal between two identical heat reservoirs efficiency. Reversible engines operate based on the second law of thermodynamics. Energy transfer in these engines is also in the reverse direction. The Carnot engine is the most efficient reversible engine. The irreversible Heat Engines are strictly less effective and efficient than the reversible heat engines. But they are more realistic because the internal irreversibilities are almost unavoidable in real applications. Here are some examples of irreversible engines: Friction, Reactions in chemistry, and Deformation due to plasticity.
