JEE Important Chapter - Vector Algebra

Algebraic operations on vectors are included in vector algebra. Vector algebra is the branch of mathematics that deals with the magnitude and direction of vectors. In physics and engineering, vector algebra is used to execute addition and multiplication operations on physical values represented as vectors in three-dimensional space.

In this article, we will learn about vector algebra and its operations, types of vectors along with the help of examples and practice questions for better understanding and knowledge.  

JEE Main Maths Chapter-wise Solutions 2022-23 

Important topics of Vector Algebra 

• Vectors

• Types of Vectors

• Vector Algebra 

• Section Formula

• Product of two Vectors 

Important Concepts of Vector Algebra 

What is Vector Algebra?

Many algebraic operations involving vectors are performed using vector algebra. The word vector comes from the Latin word vector, which means "carrier." Vectors transport information from point A to point B. The magnitude of the vector is the length of the line between two points A and B, and the direction of the vector AB is the direction of displacement of point A to point B. Euclidean vectors and spatial vectors are other names for vectors. Vectors are used in arithmetic, physics, engineering, and a variety of other professions.

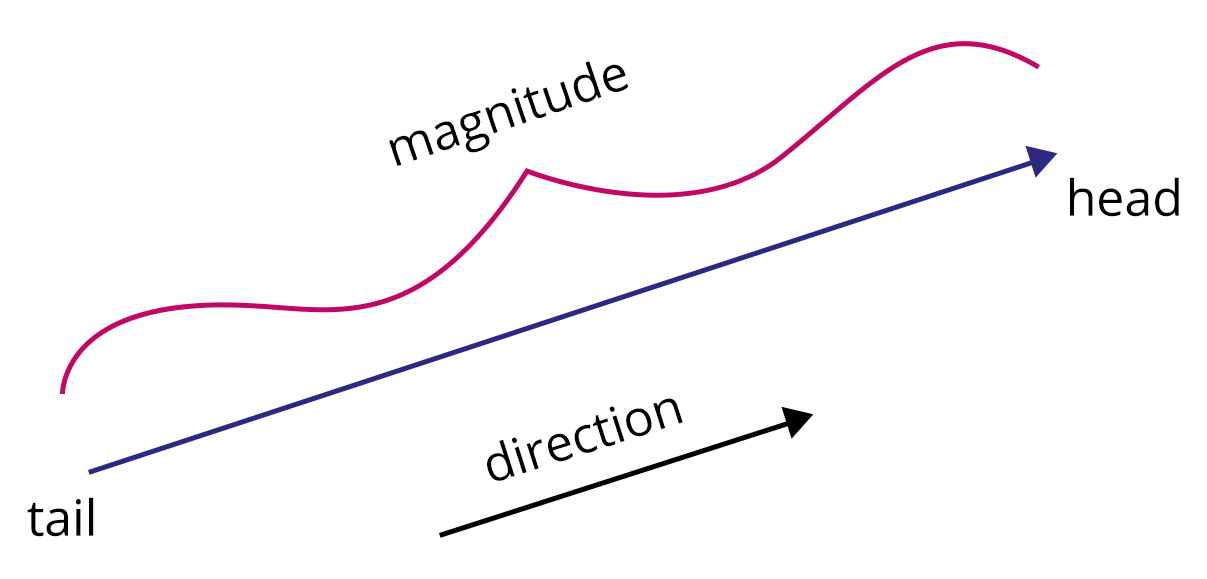
Image: Vector Components

In mathematics, a vector is a geometric entity with both magnitude and direction. Vectors have a starting point at which they begin and a terminal point that indicates the point's final position. In vector algebra, several algebraic operations such as addition, subtraction, and multiplication can be done. Many physical quantities, such as velocity, displacement, acceleration, and force, are vector values, meaning they have both a magnitude and a direction.

Representation of Vectors

Vectors are usually represented in bold lowercase such as a or using an arrow over the letter as $\vec{a}$. Vectors can also be denoted by their initial and terminal points with an arrow above them, for example, vector AB can be denoted as $\overrightarrow{AB}$. The standard form of representation of a vectors is $\vec{A}=a \hat{i}+b\hat{j}+c\hat{k}$. Here, a,b,c are real numbers and $\hat{i}, \hat{j}, \hat{k}$ are the unit vectors along the x-axis, y-axis, and z-axis respectively.

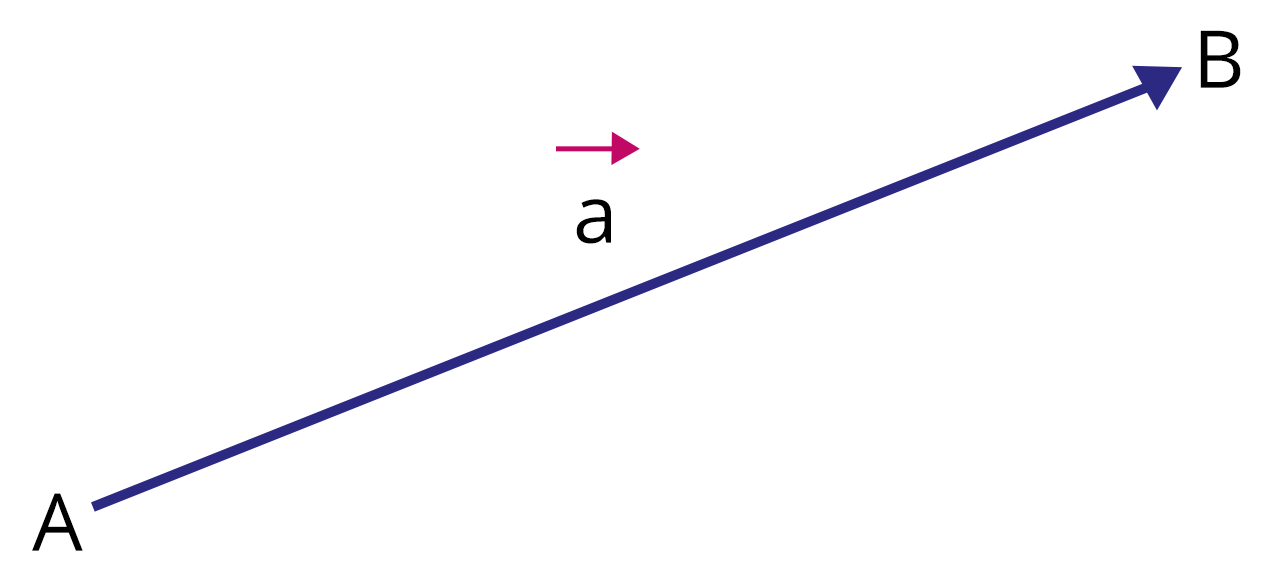
Image: Vector representation

The tail of a vector is also known as the beginning, whereas the head is known as the end. The movement of an object from one location to another is described by vectors. Vectors are represented as ordered pairs in the cartesian coordinate system. An 'n-tuple' can also be used to represent vectors in 'n' dimensions. Vectors are also identified with a tuple of components which are the scalar coefficients for a set of basis vectors and the basis vectors are denoted as e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)

Magnitude of Vectors

The square root of the sum of the squares of a vector's components can be used to calculate its magnitude. Assume, if (x,y,z) are the components of a vector A, then the magnitude formula of A is given by,

$\left | z \right |=\sqrt{x^2+y^2+z^2}$

The magnitude of a vector is a scalar value.

Types of Vectors - Vector Algebra

Different types of vectors are utilised in vector algebra for various algebraic operations. Based on their magnitude, direction, and relationships with other vectors, vectors are classified into different types. Let's look at a few different types of vectors and their properties accordingly:

Zero Vectors

Vectors that have 0 magnitudes are called zero vectors and is denoted by $\overrightarrow{0}$ = (0,0,0). The zero vector has zero magnitudes and has no direction, It is also called the additive identity of vectors.

Unit Vectors

Vector having a magnitude equal to 1 are called the unit vectors, denoted by $\hat{a}$. It is also called the multiplicative identity of vectors and the magnitude of a unit vector is 1. It is usually used to denote the direction of a vector.

Position Vectors

In three-dimensional space, position vectors are used to determine the position and direction of movement of vectors. Position vectors' magnitude and direction can be modified in relation to other bodies, and it is also known as the position vector. 

Equal Vectors

If the corresponding components of two or more vectors are identical, they are said to be equal. The magnitude and direction of equal vectors are the same. Although the initial and terminal points may differ, the magnitude and direction must be equal.

Negative Vector

A vector is said to be the negative of any other vector if they have the same magnitudes but are opposite in direction. Consider if vectors A and B have equal magnitude but opposite directions, then vector A is said to be the negative of vector B or vice-versa.

Parallel Vectors

If two or more vectors have the same direction but not necessarily the same magnitude, they are said to be parallel vectors. The angles of parallel vectors' directions differ by zero degrees. Antiparallel vectors are those whose direction angles differ by 180 degrees, i.e., antiparallel vectors have opposite directions.

Orthogonal Vectors

If the angle between two or more vectors in space is 90 degrees, they are said to be orthogonal. In other words, the dot product of orthogonal vectors is always 0. a·b = |a|·|b|cos90° = 0.

Co-initial Vectors

Co-initial vectors are two vectors that have the same initial point.

Operations in Vector Algebra

Some basic vector algebra operations can be done geometrically without the use of a coordinate system. Addition, subtraction, and multiplication by a scalar are some of the operations that can be performed on vectors. The dot product and the cross product of vectors are also two other ways of multiplying vectors. The following are the various operations in vector algebra. 

• Addition of Vectors

• Subtraction of Vectors

• Scalar Multiplication

• Scalar Triple Product of Vectors

• Multiplication of Vectors

Let us understand each of these operations in vector algebra in the below paragraphs.

Addition of Vectors

Let us consider there are two vectors P and Q, then the sum of these two vectors can be performed when the tail of vector Q meets with the head of vector A. And during this addition, the magnitude and direction of the vectors should not change. The vector addition follows two important laws, which are;

Commutative Law: P + Q = Q + P

Associative Law: P + (Q + R) = (P + Q) + R

Subtraction of Vectors

Here, the direction of other vectors is reversed and then the addition operation is performed on both the vectors given. If P and Q are the vectors for which the subtraction method must be used, we must invert the direction of another vector, such as Q, to make it -Q. The vectors P and -Q must now be added. The vectors' directions are thus opposite, but their magnitude remains the same.

P – Q = P + (-Q)

Multiplication of Vectors

The scalar multiplication is represented by kA when k is a scalar quantity multiplied by a vector A. If k is positive, the direction of vector kA is the same as the direction of vector A; however, if k is negative, the direction of vector kA is the opposite of the direction of vector A and the magnitude of the vector kA is given by |kA|.

Dot Product

A scalar product is often referred to as a dot product. Between two vectors, a dot(.) is used to symbolise it. Two equal-length coordinate vectors are multiplied to get a single integer. In other words, when two vectors are scalar products, the outcome is either a number or a scalar quantity. If P and Q are two vectors, then the dot product of both vectors is as follows:

P.Q = |P| |Q| cos θ

If P and Q are both in the same direction, i.e. θ = 0°, then;

P.Q = |P| |Q|

If P and Q are both orthogonal, i.e. θ = 90°, then;

P.Q = 0 $[$since cos 90° = 0$]$

In vector algebra, if two vectors are given as;

P = [P1,P2,P3,P4,….,Pn] and Q = [Q1,Q2,Q3,Q4,….,Qn]

Then their dot product is given by;

P.Q = P1Q1+P2Q2+P3Q3+……….PnQn

Cross Product

The multiplication sign(x) between two vectors denotes a cross product. It's a three-dimensional system with a binary vector operation. If P and Q are two independent vectors, the outcome of their cross product (P x Q) is perpendicular to both vectors and normal to the plane in which they are both located. It is represented by;

P x Q = |P| |Q| sin θ$\hat{n}$

Applications of Vector Algebra

In the fields of physics and mathematics, vector algebra has several applications. Quantities with both direction and magnitude are dealt with in vector algebra. Many quantities, such as velocity, acceleration, and force, must be represented as mathematical expressions and can be represented as vectors. The following are some examples of vector algebra applications.

• Vectors are one of the most significant factors in the study of partial differential equations and differential geometry.

• Vectors are particularly valuable in the study of many domains in physics and engineering, such as electromagnetic fields, gravitational fields, and fluid flow.

• Vector algebra is handy when finding the component of a force in a certain direction.

• Vector algebra is used in physics to determine the interaction between two or more quantities.

• The dot of one vector is the cross product of the other two vectors in the scalar triple product of vectors. In a scalar triple product, if any two vectors are equal, the scalar triple product is zero. The three vectors a, b, and c are said to be coplanar if the scalar triple product is equal to zero.

Also, a·(b × c) = b·(c × a) = c·(a × b)

List of Formulae

Solved Examples 

Example 1: Find the magnitude of the vector $\overrightarrow a$ = 5i - 3j + k, using the formula from vector algebra.

Solution:

The given vector is $\overrightarrow a$ = 5i - 3j + k.

The magnitude of the vector is |a| = $\sqrt{5^2 + (-3)^2 + 1^2} = \sqrt{25 + 9 + 1} = \sqrt{35}$

Therefore, the magnitude of the vector is $\sqrt{35}$.

Example 2: Using vector algebra concepts, find the dot product between the two vectors 2i + 3j + k, and 5i -2j + 3k.

Solution:

The two given vectors are:

$\overrightarrow a$ = 2i + 3i + k, and $\overrightarrow b$ = 5i -2j + 3k

Using the dot product we have $\overrightarrow a.\overrightarrow b$ = 2.(5) + 3.(-2) + 1.(3) = 10 - 6 + 3 = 7

Therefore, the dot product of the two vectors is 7.

Solved Problem of Previous year Question Paper 

Question 1: Let b = 4i + 3j and c be two vectors perpendicular to each other in the xy-plane. All vectors in the same plane having projections 1 and 2 along b and c respectively are given by _________.

Solution:

Let r = λb + μc and c = ± (xi + yj).

Since c and b are perpendicular, we have 4x + 3y = 0

⇒ c = ±x (i − 43j), {Because, y = $[$−4 / 3$]$x}

Now, projection of r on b = $[$r.b$]$ /$[$|b|$]$ = 1

⇒ $[$(λb + μc) . b$]$ / $[$|b|$]$

= $[$λb . B$]$ / $[$|b|$]$ = 1

⇒ λ = 1 / 5

Again, projection of r on c = $[$r.c$]$ / $[$|c|$]$ = 2

This gives μx = $[$6 / 5$]$

⇒ r = $[$1 / 5$]$ (4i + 3j) + $[$6 / 5$]$ (i − $[$4 / 3$]$j)

= 2i−j or

r = $[$1 / 5$]$ (4i + 3j) − $[$6 / 5$]$ (i − $[$4 / 3$]$j)

= $[$−2 / 5$]$ i + $[$11 / 5$]$ j

Question 2: If a, b and c are unit vectors, then |a − b|2 + |b − c|2 + |c − a|2 does not exceed

A) 4

B) 9

C) 8

D) 6

Solution:

|a − b|2 + |b − c|2 + |c − a|2 = 2 (a2 + b2 + c2) − 2 (a $\times$ b + b $\times$ c + c $\times$ a)

= 2 $\times$ 3 − 2 (a $\times$ b + b $\times$ c + c $\times$ a)

= 6 − {(a + b + c)2 − a2− b2 − c2}

= 9 − |a + b + c| 2 ≤ 9

Question 3: Let a, b and c be vectors with magnitudes 3, 4 and 5 respectively and a + b + c = 0, then the values of a . b + b . c + c . a is ________.

Solution:

Since a + b + c = 0

On squaring both sides, we get

|a|2 + |b|2 + |c|2 + 2 (a . b + b . c + c . a) = 0

⇒ 2 (a . b + b . c + c . a) = − (9 + 16 + 25)

⇒ a . b + b . c + c . a = −25

Practise Questions 

Q1. Let $\vec{a}=\hat{j}-\hat{k}$ and $\vec{c}=\hat{i}-\hat{j}-\hat{k} .$ Then the vector $\vec{b}$ satisfying $\vec{a} \times \vec{b}+\vec{c}=\overrightarrow{0}$ and $\vec{a} . \vec{b}=3$ is :

A. $-\hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}}$

B. $2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+2 \hat{\mathrm{k}}$

C. $\hat{\mathrm{i}}-\hat{\mathrm{j}}-2 \hat{\mathrm{k}}$

D. $\hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}}$

Q2. If $\overrightarrow{\mathrm{a}}=\frac{1}{\sqrt{10}}(3 \hat{\mathrm{i}}+\hat{\mathrm{k}})$ and $\overrightarrow{\mathrm{b}}=\frac{1}{7}(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-6 \hat{\mathrm{k}}),$ then the value of $(2 \overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}) \cdot[(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \times(\overrightarrow{\mathrm{a}}+2 \overrightarrow{\mathrm{b}})]$ is 1:

A.  5                    

B.  3                   

C.  – 5                   

D.  – 3

Answer: 1-A, 2-C 

Conclusion 

A vector is defined as an object that has both directions and magnitude in general. In this post, we'll look at several types of vectors, as well as vector algebra operations and applications. Also, for a better grasp of the subject, we went through some of the solved examples and previous year's problems.

Important Related Links for JEE Main 2022-23