JEE Advanced 2025 Revision Notes for Probability - Free PDF Download
One of the most scoring chapters in the JEE Advanced Maths syllabus is Probability. This chapter introduces the concepts of determining the possible events of any action and the probability of the occurrence of a particular event among them. The formulas used in this chapter to determine the probability of an event are derived from the permutation and combination principles. To understand the mathematical concept of probability, refer to the Probability JEE Advanced notes prepared by the experts.
Category: | JEE Advanced Revision Notes |
Content-Type: | Text, Images, Videos and PDF |
Exam: | JEE Advanced |
Chapter Name: | Probability |
Academic Session: | 2025 |
Medium: | English Medium |
Subject: | Mathematics |
Available Material: | Chapter-wise Revision Notes with PDF |
These notes have been prepared to offer an easier medium to understand the formulas and their derivations. All the mathematical expressions will be explained following the JEE Advanced standards to help you complete preparing this chapter in no time. Resolve doubts on your own and use these notes to recall what you have studied before an exam.
Access JEE Advanced Revision Notes Maths Probability
Probability:
The theory of probability is a branch of mathematics that deals with uncertain or unpredictable events. Probability is a concept that gives a numerical measurement for the likelihood of occurrence of an event.
An act that gives some result is an experiment.
A possible result of experiments is the set of all its outcomes. Thus, each outcome is also called a sample point of the experiment.
An experiment repeated under essentially homogeneous and similar conditions may result in an outcome that is either unique or not unique but one of the several possible outcomes.
An Experiment is Called A Random Experiment If It Satisfies the Following Two Conditions:
It has more than one possible outcome.
It is not possible to predict the outcome in advance.
The experiments that result in a unique outcome is called deterministic experiment.
Sample space is a set consisting of all the outcomes, and its cardinality is given by $n(S)$.
Any subset ‘${\rm E}$’ of a sample space for an experiment is called an event.
The empty set $\phi$ and the sample space $S$ describe events. $\phi$ is called an impossible event, and $S$, the whole sample space, is called the sure event.
Whenever an outcome satisfies the conditions, given the event, we say that the event has occurred.
If an event ${\rm E}$ has only one sample point of a sample space, It is called a sample event. In the experiment of tossing a coin, the sample space is { H, T } and the event of getting an {H} or a {T} is simple.
Subset: A subset of the sample space with more than one element is called a compound event. In throwing a dice, the appearance of odd numbers is a compound event because ${\rm E} = \{ 1,3,5\}$ has 3 sample points or elements.
Events are said to be equally likely if we have no reason to believe that one is more likely to occur than the other. The outcomes of an unbiased coin are equally likely.
Probability of an event, $E$, is the ratio of the number of elements in the event to the number of elements in the sample space.
$P(E) = \dfrac{{n(E)}}{{n(S)}}$
$0 \leqslant P(E) \leqslant 1$
Independent Events: Two or more events are said to be independent if the occurrence or non-occurrence of any of them does not affect the probability of occurrence or non-occurrence of the other event.
The complement of an event $A$ is the set of all outcomes which are not in $A$. It is denoted by ‘$A$’.
Events $A$and $B$ are mutually exclusive if and only if they have no elements in common.
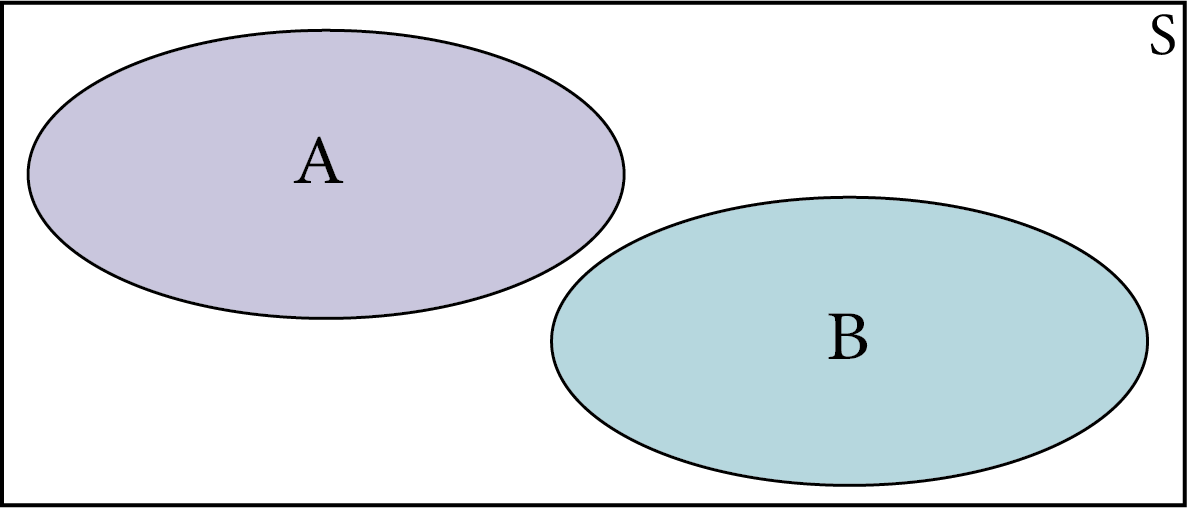
Mutually Exclusive
$P(A \text { or } B)=P(A)+P(B)$
$P(A \text { and } B)=0$
When every possible outcome of an experiment is considered, the events are called exhaustive events.
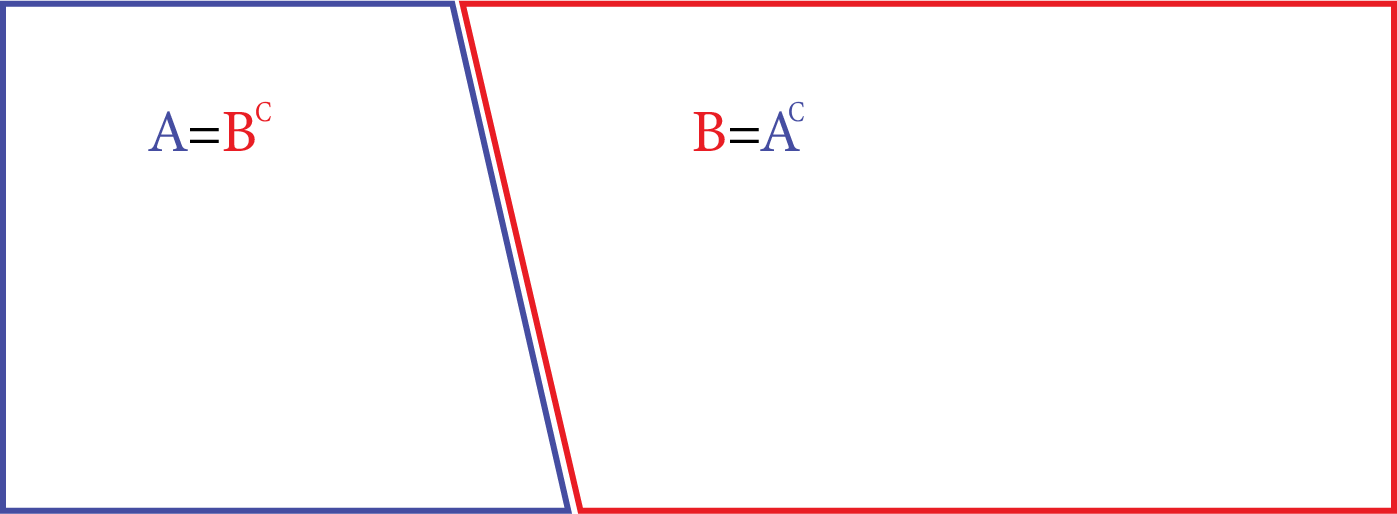
Exhaustive Event
Events ${E_1},{E_2},.........,{E_n}$are mutually exclusive and exhaustive if
${E_1} \cup ,{E_2} \cup ,........., \cup {E_n} = S$and${E_i} \cap {E_j} = \varphi $, for every distinct pair of events.
When the sets $A$ and $B$ are two events associated with a sample space, then $A \cup B$is the event either $A$or $B$ or both.
Therefore event $A$ or B =$A \cup B$
=$\{ \omega :\omega \in A$ or $\omega \in B\}$
If $A$ and $B$ are events, then the event A $A$ and $B$ are defined as the set of all the outcomes favourable to both $A$ and $B$, that is, $A$ and $B$ is the event $A \cap B$. This is represented diagrammatically as follows

A Intersection B
If $A$ and $B$ are events, then the event $A$-$B$ is defined to be the set of all outcomes which are favourable to $A$ but not to $B$. $A - B = A \cap B$ $= \{ x:x \in A$ and $x \notin B\} $.
This is represented diagrammatically as:
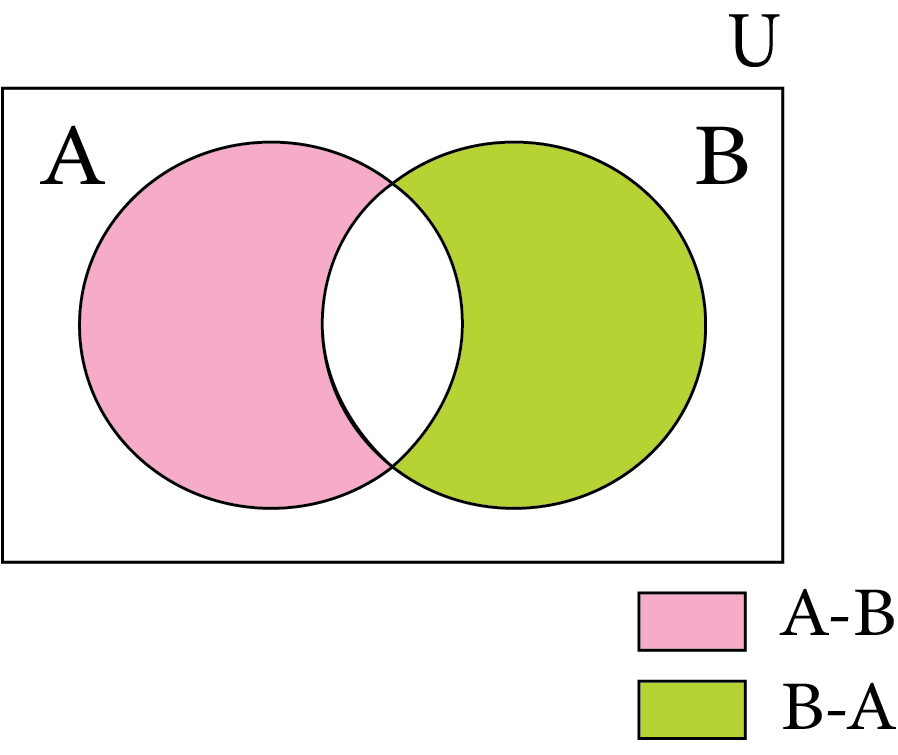
A but not B
If $S$is the sample space of an experiment with n equally likely outcomes $S = \{ {w_1},{w_2},.........{w_n}\} $then
$P({w_1}) = P({w_2}) = P({w_n}) = n$.
$\sum\limits_{i = 1}^n {P({w_1}) = 1} $
So $P({w_n}) = 1/n$
Let S be the sample space of a random experiment. the probability P is a real value function with domain the power set of S and range the interval [0,1] satisfying the axioms that:
For any event, $E, P(E)$ is greater than or equal to 1.
$p(S) = 1$
Number $P(\omega I)$associated with sample point $\omega i$such that $0 \leqslant P(\omega i) \leqslant 1$
The Additional Theorem of Probability: If $A$ and $B$ be any two events, then the probability of occurrence of at least one of the events $A$and $B$is given by
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
If $A$and $B$are mutually exclusive events then $P(A \cup B) = P(A) + P(B)$
Additional Theorem for Three Events
$P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C) - P(A \cap C) + P(A \cap B \cap C)$
If $E$ is any event and $E'$ be the complement of event $E$, then
$P(E') = 1 - P(E)$
Probability of difference of events: Let$A$ and $B$be events.
Then, $P(A - B) = P(A) - P(A \cap B)$
Additional theorem in terms of difference of events:
$P(A \cup B) = P(A - B) + P(B - A) + P(A \cap B)$
The Conditional Probability:
If $E$ and $F$ are two events associated with the same sample space of a random experiment, the conditional probability of the event$E$, given the occurrence of the event$F$is given by
${\text{P}}({\text{E}}\mid {\text{F}}) = \dfrac{{{\text{ Number of elementary events favourable to E}} \cap {\text{F}}}}{{{\text{ Number of elementary events which are favourable to F}}}}$
$= \dfrac{{n({\text{E}} \cap {\text{F}})}}{{n(\;{\text{F}})}}$
${\text{P}}({\text{EF}}{\text{F}}) = \dfrac{{\dfrac{{n({\text{E}} \cap {\text{F}})}}{{n(\;{\text{S}})}}}}{{\dfrac{{n(\;{\text{F}})}}{{n(\;{\text{S}})}}}} = \dfrac{{{\text{P}}({\text{E}} \cap {\text{F}})}}{{{\text{P}}({\text{F}})}}$
Properties of Probability:
Let $E$ and $F$ be events of a sample space $S$ of an experiments,
Then we have
1) $P(\dfrac{S}{F}) = P(\dfrac{F}{F}) = 1$
2) $0 \leqslant P(\dfrac{E}{F}) \leqslant 1,$
3) $P(\dfrac{{{E^1}}}{F}) = 1 - P(\dfrac{E}{F})$
4) $P\left( {\dfrac{{(E \cup F)}}{G}} \right) = P(\dfrac{E}{G}) + P(\dfrac{F}{G}) - P\left( {\dfrac{{(E \cap F)}}{G}} \right)$
Multiple Theorem on Probability:
$P(E \cap F) = P(E)$ $P\left( {\dfrac{F}{E}} \right),P(E) \ne 0$
$P(E \cap F) = P(F)$ $P\left( {\dfrac{E}{F}} \right),P(E) \ne 0$
If $E$&$F$ are independent, then:
$P(E \cap F) = P(E)$ $P(F)$
$P(E/F) = P(E)$,$P(F) \ne 0$
$P(F/E) = P(F)$,$P(F) \ne 0$
Theorem of Total Probability:
The event ${E_1},{E_2},{E_3},..............,{E_n}$ has non-zero probability. Let $A$ be any event associated with $S$,
Then $P(A) = P({E_1})P(\dfrac{A}{{{E_1}}}) + P({E_2})P(\dfrac{A}{{{E_2}}}) + ......................... + P({E_n})P(\dfrac{A}{{{E_n}}})$
Baye’s Theorem:
If ${E_1},{E_2},{E_3},..............,{E_n}$ are the events which constitute a partition of S
i.e., ${E_1},{E_2},{E_3},..............,{E_n}$ are pair wise disjoint
And ${E_1} \cup {E_2} \cup ................... \cup$
${E_n} = S\& A$ be ant event with non-zero probability.
Then
$P(\dfrac{{{E_i}}}{A}) = \dfrac{{P(Ei)P(\dfrac{A}{{{E_i}}})}}{{\sum\nolimits_{j - 1}^n {P(Ej)P(\dfrac{A}{{{E_j}}})} }}$
A random variable is a real valued function whose domain is the sample space of random experiment.
The probability distribution of a random variable $X$is the system of nos.
$X:$ ${x_1}$ , ${x_2}$ …………………………….. ${x_n}$
$P(X):$ ${p_1}$ , ${p_2}$……………………………… ${p_n}$
Where ${p_i} > 0$,$\sum\nolimits_{i = 1}^n {{p_i}} = 1$,$i = 1,2,....................,n$
Let $X$be a random variable whose possible value ${x_1},{x_2},.........,{x_n}$ occur with probabilities
${p_1},{p_2},.........,{p_n}$ Respectively. The mean of $X$, denoted by $\mu $is the No. $\sum\nolimits_{i = 1}^n {xipi} $.
The mean of random variable $X$is also called the expectation of$X$, denoted by$E(X)$.
Let $X$ be a random variable whose possible values, ${x_1}$,${x_2}$,……………………………..,${x_n}$ occur with probabilities. $p({x_1}),p({x_2}),............,p({x_n})$.
Let $\mu$ = $E(X)$ be the mean of $X$. The variance of $X$, denoted by Variable($X$) or $\sigma _\pi ^2$ is defined as
$\sigma _\pi ^2 = Var(X) = \sum\nolimits_{i = 1}^n {{{(xi - \mu )}^2}} p(xi)$ or
$\sigma _\pi ^2 = E{(X - \mu )^2}$
The non-negative no,
${\sigma _\pi } = \sqrt {Var(X)} $=$\sqrt {\sum\nolimits_{i = 1}^n {} } $${(xi - \mu )^2}p(xi)$, is called the standard deviation of the random variable X.
Var $(X) = E({X^2}) - {[E(X)]^2}$
Trails of a random experiment are called Bernoulli trials if they satisfy the following conditions:
There should be a finite number of trials.
The trial should be independent.
Each trial has exactly two outcomes: success or failure.
The probability of success remains the same in each trial.
For binomial distribution $B(n,p)$, $P(X = x) = {}^n{C_x}q{}^{n - x}{p^x},x = 1,2,3,........,n$ & (q=1-p
Mean = $np$, and Varience =$npq$
Standard deviation= $\sqrt {npq}$
Example Problems:
1. An insurance company insured 2000 scooter drivers, 4000 car drivers, and 6000 truck drivers. The probability of an accident involving a scooter, a car, and a truck is 0.01, 0.03, and 0.15, respectively. If a driver meets an accident, what is the chance that the person is a scooter driver? What is the importance of insurance in everybody’s life?
Ans: Let A be the event the insured person meets with an accident and ${E_1}$, ${E_2}$ and ${E_3}$ are the events that the person is a scooter. Car and truck driver respectively. Then we have to find$P\left( {\dfrac{{{E_1}}}{A}} \right)$.
Total number of insured persons=2000+4000+6000=12000.
$P({E_1}) = \dfrac{{2000}}{{12000}} = \dfrac{1}{6};$
$P({E_2}) = \dfrac{{4000}}{{12000}} = \dfrac{1}{3};$
$P({E_3}) = \dfrac{{6000}}{{12000}} = \dfrac{1}{2};$
Also $P\left( {\dfrac{A}{{{E_1}}}} \right) = 0.01;$
$P\left( {\dfrac{A}{{{E_2}}}} \right) = 0.03;$
$P\left( {\dfrac{A}{{{E_3}}}} \right) = 0.15;$
Hence, by Baye’s theorem we have
$P\left( {\dfrac{A}{{{E_1}}}} \right) = \dfrac{{P\left( {\dfrac{A}{{{E_1}}}} \right)P({E_1})}}{{P\left( {\dfrac{A}{{{E_1}}}} \right)P({E_1}) - P\left( {\dfrac{A}{{{E_2}}}} \right)P({E_2}) - P\left( {\dfrac{A}{{{E_3}}}} \right)P({E_3})}}$
$= \dfrac{{0.01 \times \dfrac{1}{6}}}{{0.01 \times \dfrac{1}{6} - 0.03 \times \dfrac{1}{3} - 0.15 \times \dfrac{1}{2}}} = \dfrac{1}{{52}}$
2. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond. Is it better not to tell anyone about the loss of the card while playing?
Ans:
Let ${E_1},{E_2},{E_3},{E_4}$and A be the events defined as follows,
${E_1} = $ The missing card is a diamond
${E_2} = $ The missing card is not diamond
$A$ =Two drawn card are of diamond
Now $P({E_1}) = \dfrac{{13}}{{52}} = \dfrac{1}{4}$
$P({E_2}) = \dfrac{1}{4}$
$P\left( {\dfrac{A}{{{E_1}}}} \right) = $Probability of drawing of second heart cards when one diamond card id missing
$= \dfrac{{C(12.2)}}{{C(51.2)}} = \dfrac{{12}}{{51}}.\dfrac{{11}}{{50}}$
Similarly$P\left( {\dfrac{A}{{{E_2}}}} \right) = \dfrac{{C(13.2)}}{{C(52.2)}} = \dfrac{{12}}{{51}}.\dfrac{{12}}{{50}}$
$P\left( {\dfrac{{{E_2}}}{A}} \right) = \dfrac{{P({E_1}).P\left( {\dfrac{\Delta }{{{E_1}}}} \right)}}{{P({E_1}).P\left( {\dfrac{\Delta }{{{E_1}}}} \right) + P({E_2}).P\left( {\dfrac{\Delta }{{{E_2}}}} \right)}}$
$= \dfrac{{\dfrac{1}{4}.\dfrac{{12}}{{51}}.\dfrac{{11}}{{50}}}}{{\dfrac{1}{4}.\dfrac{{12}}{{51}}.\dfrac{{11}}{{50}} + \dfrac{3}{4}.\dfrac{{13}}{{51}}.\dfrac{{12}}{{50}}}} = \dfrac{{1.12.11}}{{1.12.11 + 3.13.12}} = \dfrac{{11}}{{11 + 39}} = \dfrac{{11}}{{50}}$
No, when we are playing any game it should be played honestly.
3. A man is known to speak the truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is a six, and write at least one drawback of telling a lie.
Ans: The event that six occurs and ${S_2}$ be the event that six does not occur.
Then $P({S_1}) = $Probability that six occurs $= \dfrac{1}{6}$
$P({S_2}) = $Probability that six does not occur $= \dfrac{5}{6}$
$P(E|{S_2}) = $Probability that the man reports that six occurs when six has
Not actually occurred on the die.
=Probability that the man does not speak the truth =$1 - \dfrac{3}{4} - \dfrac{1}{4}$
Thus by Baye’s theorem, we get
$P({S_1}/E) = $Probability that the report of the man that six has occurred is
Actually a six
$= \dfrac{{P({S_1})P\left( {\dfrac{E}{{{S_1}}}} \right)}}{{P({S_1})P\left( {\dfrac{E}{{{S_1}}}} \right) + P({S_2})P\left( {\dfrac{E}{{{S_2}}}} \right)}}$
Hence, the required probability is $= \dfrac{3}{8}$.
Importance of Maths Probability
There are many outcomes of an event we see every day. For instance, if we roll a dice once, the outcome can be of six types as there are six faces on it. This chapter will introduce the concepts of how to determine the probable outcomes of specific events. It will also teach how to identify such events when the cases change.
The outcomes of an event can be calculated using the formulas of permutation and combination. Based on the interpretation of outcomes, the probability of a particular outcome of an event can be determined.
All these concepts have applications in various fields. This chapter is also important as the concepts of probability are used in statistics too. Hence, students will need to learn how to observe an event and determine its outcomes in this chapter.
These revision notes will help you to get a clear idea of how the formulas are derived for the calculation of outcomes in an event, and learn the actual meaning of terms such as independent events, dependent events, complementary events, likely events, etc., from the explanation given in the chapter. To make the Probability JEE Advanced revision easier, refer to these notes prepared by our subject experts.
Benefits of Probability JEE Advanced Revision Notes
These revision notes will explain the basic and advanced concepts of this chapter in a simple way. These notes will help you to understand the concepts and find out what is not explained in this chapter properly.
The concise format of the revision notes will help you complete preparing this chapter faster. You will also learn how simply all the formulas and derivations can be explained.
Take a step ahead in your JEE Advanced preparation using these fundamental notes. You can solve the sample questions to assess your knowledge of this chapter. Thus, you will be able to gauge your preparation with these revision notes.
Download Probability JEE Advanced Notes Free PDF
Students can download the Probability revision notes PDF from Vedantu or refer to the notes online. These notes will certainly provide the simplest explanation of the mathematical concepts of Probability and help you learn and practice the sums more efficiently. So refer to these notes to take a step ahead in your JEE Advanced preparation.
Important Related Links for JEE Main and JEE Advanced
FAQs on JEE Advanced 2025 Revision Notes for Probability
1. How can we represent the expression of probability?
The expression to calculate Probability can be written in the form of a ratio of the occurrence of a favourable outcome to the total number of possible outcomes for an event.
2. What is a sure event?
A sure event is defined in terms of Probability. As it is sure, its Probability is one.
3. How many classifications of Probability are there?
There are three classifications of Probability.
Axiomatic Probability
Experimental Probability
- Theoretical Probability
4. In how many ways three dice can be thrown?
As per the outcomes, the number of ways of throwing three dices is = 6 x 6 x 6 = 216.

























