JEE - Integral Calculus and Differential Equations

The branch of calculus where we study integrals and their properties is known as integral calculus. Integration is a crucial concept because it is the inverse of differentiation or we can say antiderivative. The fundamental theorem of calculus connects integral and differential calculus. In this article, you will learn about integral calculus, its types, formulas, examples, and applications.

Important Topics of Integral Calculus and Differential Equations

• Integration

• Integral Calculus

• Differential Equations

• Integration by Parts Rule

• First Order Differential Equation

• Linear Differential Equations

• Partial Fractions

• Fundamental Theorem of Integral Calculus

• Types of Differential Equations

• Order of Differential Equation

• Degree of Differential Equation

• Differential Equations Solutions

• Applications

Important Concepts of Integral Calculus

What is Integral Calculus

Integrals are the values of the function found through the integration process. Integration is the process of obtaining f(x) from f'(x). The function f(x) is referred to as an antiderivative or integral of f'(x) in this case. The anti-derivative or primitive of the function f'(x) is referred to as f(x) in integral calculus. Anti-differentiation or integration is the term for the process of locating anti-derivatives (inverse of differentiation).

Example: (1) $f(x) = x^2$

Then the derivative of f(x) will be,

$f(x) = f^\prime(x) = 2x = g(x)$

Then antiderivative of the above equation will be $g(x) = \int{g(x)} = x^2 + c$ 

(2) $f(x) = \sin x$

We can also solve other ways,

$\dfrac{d}{dx}\sin x = \cos x + c$

Integral Calculus Formulas

In general, integrals are classified into two categories:

1. Definite Integral

2. Indefinite Integral

Definite Integrals

On the interval [a, b], the definite integral of a real-valued function f(x) with respect to a real variable x is expressed as

$\int_{a}^{b} f(x) dx = F(b) - F(a)$

Where,

a = Lower limit

b = Upper limit

f(x) = Integrand

dx = Integrating agent

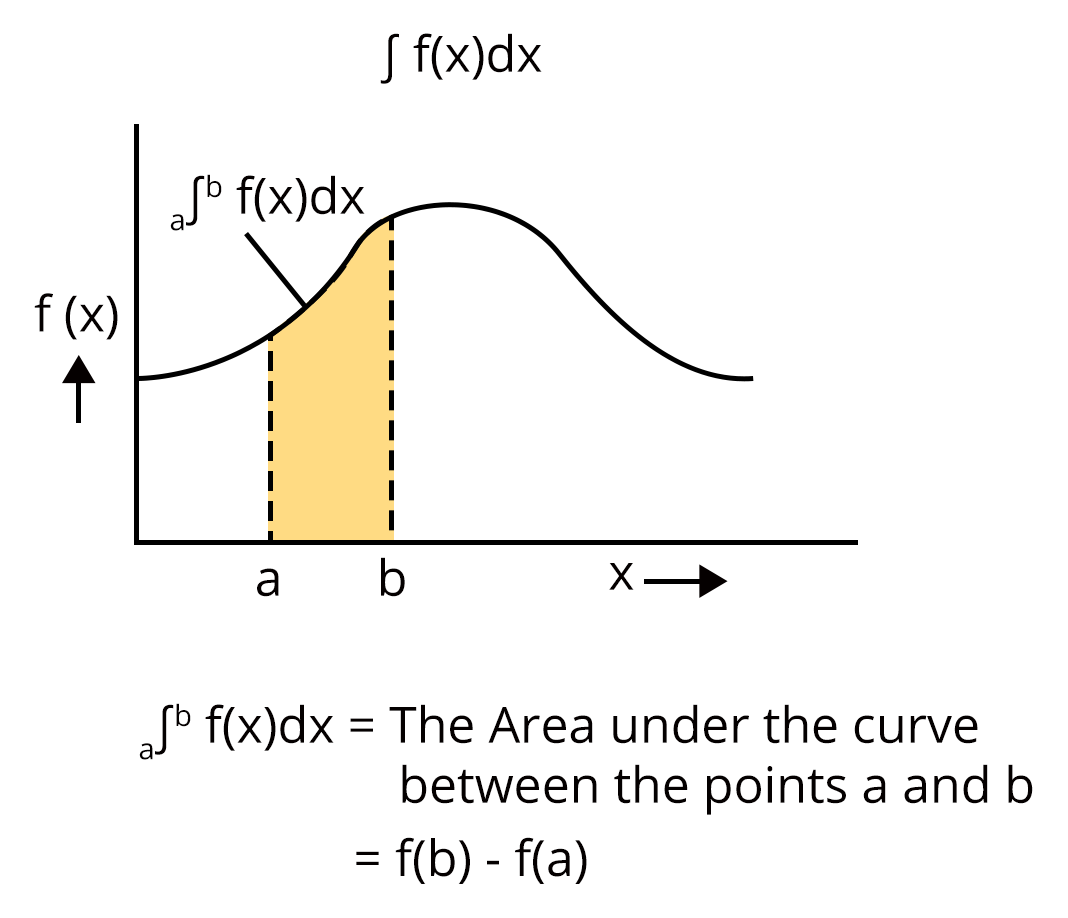
Definite Integral Properties

• $\int_{a}^{b} f(x) dx = \int_{a}^{b} f(t) d(t)$

• $\int_{a}^{b} f(x) dx = -\int_{b}^{a} f(x) dx$

• $\int_{a}^{a} f(x) dx = 0$

• $\int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx+\int_{c}^{b} f(x) dx$

• $\int_{a}^{b} f(x) dx = \int_{a}^{b} f(a+b-x) dx$

• $\int_{0}^{a} f(x) dx = f(a-x) dx$

Definite Integral by Parts

• $\int_{0}^{2 a} f(x) dx=\int_{0}^{a} f(x) dx+\int_{0}^{a} f(2 a-x) dx$

• $\int_{0}^{2 a} f(x) dx=2 \int_{0}^{a} f(x) dx \ldots \text { if } f(2 a-x)=f(x)$

• $\int_{0}^{2 a} f(x) dx=0 \ldots \text { if } f(2 a-x)=-f(x)$

• $\int-a^{a} f(x) dx=2 \int_{0}^{a} f(x) dx \ldots$ if $f(-x)=f(x)$ or it is an even function 

• $\int_{-a}^{a} f(x) dx=0$... if $f(-x)=-f(x)$ or it is an odd function

Indefinite Integrals

The term "indefinite integral" refers to an integral that has no upper or lower limit.

In General, If F(x) is any anti-derivative of f(x), the most general antiderivative of f(x) is called an indefinite integral and is denoted,

$\int{f(x)}dx = F(x) + C$

Indefinite Integral Properties

• $\int f^{\prime}(x) dx=f(x)+C$

• $\int f(x) dx-\int g(x) dx={C}$ OR $\int f(x) dx=\int g(x) dx+{C}$

• $\int[f(x)+g(x)] dx=\int f(x) dx+\int g(x) dx$

• $\int p f(x) dx=p \int f(x) dx$

• For a finite number of functions $f_{1}, f_{2} \ldots . f_{n}$ and the real numbers $p_{1}, p_{2} \ldots p_{n}$, we have

$\int\left[p_{1} f_{1}(x)+p_{2} f_{2}(x) \ldots . .+p_{n} f_{n}(x)\right] dx=p_{1} \int f_{1}(x) dx+p_{2} \int f_{2}(x) dx+\ldots . .+p_{n} \int f_{n}(x) dx$

Indefinite Integral Formulas

Standard Indefinite Integral Calculus Formulae:

Fundamental Theorem of Integral Calculus

There are two fundamental theorems of integral calculus:

First Fundamental Theorem

Let $f$ be a continuous function on the closed interval $[a, b]$ and let $A(x)$ be the area function. Then $A^\prime(x) = f(x)$, for all $x \in [a, b]$

$F(x) = \int_{a}^{x}f(t) dt$

Then $F$ is uniformly continuous on $[a, b]$ and differentiable on the open interval $(a, b)$, and

$F^\prime(x) = f(x)\,\  \forall x \in (a, b)$

Here, the $F^\prime(x)$ is a derivative function of $F(x)$.

Second Fundamental Theorem

The second fundamental theorem of calculus states that if the function "f" is continuous on the closed interval [a, b], and F is an indefinite integral of a function "f" on [a, b], then

$F(b)- F(a) = \int_{a}^{b} f(x) dx$.

The integral of f(x) with respect to x is indicated by the R.H.S. of the equation.

The integrand is f(x) and the integrating agent is dx, 'a' denotes the integral's upper limit, while 'b' denotes the integral's lower limit.

A definite integral's function has a single value. The limit of a sum can be used to describe the definite integral of a function.

Corollary

When calculating the definite integral of a function f for which an antiderivative F is known, the fundamental theorem is usually used. The corollary allows continuity on the entire interval if f is a real-valued continuous function on [a, b] and F is an antiderivative of f in [a, b].

$\int_{a}^{b} f(t) dx = F(b)- F(a)$

Integration by Parts

Integration by parts is a technique for combining the output of two or more functions. The two $f(x)$ and $g(x)$ functions to be integrated are of the form $\int{f(x) \cdot g(x)}$. As a result, it's referred to as a product rule of integration. The first function, f(x), is chosen because its derivative formula exists, while the second function, g(x), is chosen because an integral of such a function exists.

$\int f(x) \cdot g(x) dx=f(x) \int g(x) dx-\int f^{\prime}(x) \cdot\left(\int g(x) dx\right) dx$

If we consider f to be the first function and g to be the second, we can pronounce this formula as:

The integral of the product of two functions = (first function) × (integral of the second function) – Integral of {(differential coefficient of the first function) × (integral of the second function)}

Integration By Parts Formula

If u and v are two differentiable functions of the same variable x, Then, according to the product differentiation rule, we have;

$\dfrac{d}{dx}(u v)=u\dfrac{dv}{dx}+v\dfrac{du}{dx}$

Integrating both sides, we get;

$u v=\int u \dfrac{dv}{dx} dx+\int v \dfrac{du}{dx} dx$

or

$\int u \dfrac{dv}{dx} dx=u v-\int v \dfrac{du}{dx} dx$ —(1)

Let us consider, $u=f(x)$ and $\dfrac{dv}{dx}=g(x)$

Thus,the above equation becomes

$\dfrac{du}{dx}=f^{\prime}(x)$ and $v=\int g(x) dx$

On substituting in equation 1, we get 

$\int f(x) g(x) dx=f(x) \int g(x) dx-\int\left[\int g(x) dx\right] f^{\prime}(x) dx$

or

$\int f(x) g(x) dx=f(x) \int g(x) dx-\int\left[f^{\prime}(x) \int g(x) dx\right] dx$

Integration by Partial Fractions

Integration by partial fractions is a method for decomposing and integrating a rational fraction with complex terms in the denominator. We calculate and decompose the expression into simpler terms using partial fractions so that we can easily calculate or integrate the resulting expression.

Forms of Integration by Partial Fractions

Area Under the Curve

A definite integral between two points is used to find the area under a curve between two points. Integrate y = f(x) between the limits of a and b to find the area under the curve y = f(x) between x = a and x = b. This area can be calculated by integrating within certain bounds.

Formula for Area under the Curve $= \int_{a}^{b} f(x)dx$

Important Concepts of Differential Equations

What is a Differential Equation?

The differential equation is an equation containing one or more derivatives, where derivatives are terms describing the rate of change of quantities that vary continuously. In general, the solution of the differential equation is an equation that expresses the functional dependence of one variable on more than one variable. It typically includes constant terms that are not present in the original differential equation. In applications, functions typically represent physical quantities, derivatives represent their rate of change, and the differential equation determines the relationship between the two. The solution of the differential equation generates a function that can be used to predict the behavior of the original system, at least under some constraints.

Types of Differential Equations

Here are some of the different types of differential equations:

• Homogeneous Differential Equations

• Nonhomogeneous Differential Equations

• Ordinary differential equations

• Partial differential equations

• Nonlinear differential equations

• Linear Differential Equations

Order of Differential Equation

The order of the highest derivative is the order of a differential equation. Below are some examples for different orders of the differential equation.

• (d2y/dx2)+ 2 (dy/dx) + y = 0. The order is 2.

• (dy/dt) + y = kt. The order is 1.

First Order Differential Equation

A differential equation of the first order is an equation in which f(x, y) is a function of two variables defined in the XY-plane field. The equation is of the first order since only the first derivative dy/dx is involved (and not higher-order derivatives).

dy/dx = f(x, y) = y'

Second-Order Differential Equation

An equation of the form which is linear in y and its derivatives is called a second-order linear differential equation.

P(x)y''(x) + Q(x)y'(x) + R(x)y(x) = G(x)

Degree of Differential Equation

In the differential equation given, the degree of the differential equation is defined by the power of the highest order derivative. For the degree to be defined, the differential equation must be a polynomial equation in derivatives.

Ex: d4y/dx4 + (d2y/dx2)2 – 3dy/dx + y = 9

Differential Equations Solutions

There are two methods of finding solutions for differential equations:

1. Separation of Variables: This method is used when the given differential equation can be written in the form of dy/dx = f(y)g(x), where the function f is the function of y only and the function g is the function of x only. Rewrite this problem as 1/f(y)dy = g(x)dx with an initial condition and then integrate it on both sides.

2. Integrating Factor: This method is used when a given differential equation can be written in the form of dy/dx + p(x)y = q(x) where both the function p and q are functions of x only.

Differential equations of the first order are of the form y' + P(x)y = Q (x). Where P and Q are the functions of x and the first derivative of y respectively. The differential equation of the higher-order is an equation containing derivatives of an unknown function that can be a partial or ordinary derivative.  It can be represented in any order.

Applications

• Exponential Decay - Radioactive Material.

• Falling Object.

• Newton's Law of Cooling.

• RL circuit.

• Exponential Growth - Population.

• Using differential equations, the motion of waves or a pendulum can also be represented.

Ordinary Differential Equations

An equation with only one independent variable and one or more of its derivatives with respect to the variable is referred to as an Ordinary Differential Equation which is also known as ODE.

$y^\prime,y^{\prime\prime}, …. y^n ,…$ with respect to $x$.

Types of Ordinary Differential Equations:

1. Autonomous Ordinary Differential Equations

An autonomous differential equation is a differential equation that does not depend on a variable, such as x.

2. Linear Ordinary Differential Equations

Linear ordinary differential equations are differential equations that can be written as linear combinations of the derivatives of y. These are further divided into two categories:

• Homogeneous linear differential equations

If the degree of $f(x,y)$ and $g(x,y)$ is the same, a differential equation of the form $f(x,y)dy = g(x,y)dx$ is said to be a homogeneous differential equation.

$\dfrac{dy}{dx}=F(x, y)=g\left(\dfrac{y}{x}\right)$

• Non-homogeneous linear differential equations

A second-order linear nonhomogeneous differential equation is represented by:

$y^{\prime}+p(t)y^\prime+q(t)y = g(t)$, where g(t) is a non zero function.

3. Non-linear Ordinary Differential Equations

A non-linear ordinary differential equation is one in which the differential equations cannot be written in the form of linear combinations of the derivatives of y.

Steps to Solve Homogeneous Differential Equations

Given the differential equation is,

$\dfrac{dy}{dx}=F(x, y)=g\left(\dfrac{y}{x}\right)$

We use the substitution $y = v\cdot x$ to solve a homogeneous differential equation of the form $\dfrac{dy}{dx} = f(x, y)$. This substitution makes it simple to integrate and solve. With respect to x, the differentiation of $y = vx$ yields $\dfrac{dy}{dx} = v + x \cdot \dfrac{dv}{dx}$.

Now, substitute the value of $\dfrac{dy}{dx}$ in the above expression,

$\dfrac{dy}{dx} = f(x, y) = g\left(\dfrac{y}{x}\right)$

$v+x \dfrac{d v}{dx}=g(v)$

$\Rightarrow x \dfrac{d v}{dx}=g(v)-v$

Separating the variables x and v, we get

$\dfrac{d v}{g(v)-v}=\dfrac{dx}{x}$

Integrating both sides of the equation, we get

$\int \dfrac{d v}{g(v)-v} d v=\int \dfrac{dx}{x}+C$

$\int \dfrac{d v}{g(v)-v} d v=log x+C$

Variable Separable Differential Equations

Differential equations in terms of (x,y) in which the x-terms and y-terms can be separated to different sides of the equation. As a result, each variable can be easily integrated to form a differential equation solution.

A general form of the equations is $\dfrac{dy}{dx} = f(x) g(y)$

Other forms of separable differential equations are:

$f(x) dx = g(y) dy$

$\dfrac{dy}{dx} = \dfrac{f(x)}{g(y)}$

$\dfrac{dy}{dx} = f(x) g(y)$

$g(y) \dfrac{dy}{dx} = f(x)$

Method of Solving Separation of Variables:

Step 1: Write the derivative as a product of individual variable functions, e.g., 

$\dfrac{dy}{dx} = f(x) g(y)$

Step 2: Write the variables on each side of the equality

$\dfrac{dy}{g(y)} = f(x) dx$

Step 3: Integrate both sides and find the value of y, and thus the general solution of the separable differential equation

$\int{\dfrac{dy}{g(y)}} = \int{f(x) dx}$

First Order Differential Equation

A first order differential equation is one in which the maximum order of a derivative is one and in which no other higher-order derivative can appear.

$F(x, y, y^\prime) = 0$ is a first-order differential equation

Where, 

$y$ - is a dependent variable

$x$ - is an independent variable

and $y^\prime$ - appears explicitly in the differential equation.

It can also be written as $F(t, f(t), f^\prime(t)) = 0$

Where, $f(t)$ - solution of the differential equation.

Linear First Order Differential Equation

$y^\prime + y P(x) = Q(x)$ or $\dfrac{dy}{dx} + y P(x) = Q(x)$ is a linear first-order differential equation in which $y, P,$ and $Q$ are functions of $x$, and $y^\prime$ is the first-order derivative of $y$. Because the degree of the derivative in such differential equations is one, they are referred to as linear first order differential equations. Such equations can be solved using the integrating factors method.

Using Integrating Factors to Solve a First-Order Differential Equation

The integrating factors method can be used to solve a first order differential equation of the form $\dfrac{dy}{dx} + y P(x) = Q(x)$. To find the general solution of the differential equation, we can use the following steps:

Step 1: Reduce the first order differential equation to $\dfrac{dy}{dx} + y P(x) = Q(x)$

Step 2: Calculate the integrating factor, $I.F. = e^{\int{P(x) dx}}$.

Step 3: Multiply the I.F. by the differential equation $\dfrac{dy}{dx} + y P(x) = Q(x)$ to get $\dfrac{d(y \times I.F.)}{dx} = Q(x) \times I.F$.

Step 4: To obtain the general solution, integrate both sides of the equation.

Note: 

The first order differential equation has important applications in Newton's law of cooling, growth and decay models, and electric circuits.

The separation of variables, integrating factor, and variation of parameters method can be used to solve first-order differential equations.

Examples on Integral Calculus:

Example 1: Evaluate $\int_{2}^{3} x^{4} dx$

Ans: Let us consider the equation to be $I=\int_{2}^{3} x^{4} dx$

As we know the integration form of $x^n$ is $\dfrac{x^{n+1}}{n+1}$

So, on integrating, we get

$\int x^{4} dx=\dfrac{x^{5}}{5}$

Now applying the limits we get

$I=\int_{2}^{3} x^{4} dx=\left[\dfrac{x^{5}}{5}\right]_{2}^{3}$

$I=\dfrac{\left(3^{5}\right)}{5}-\dfrac{\left(2^{5}\right)}{5}$

$I=\dfrac{243}{5}-\dfrac{32}{5}$

$I=\dfrac{243-32}{5}$

$I=\dfrac{211}{5}$

Therefore, $\int_{2}^{3} x^{2} dx=\dfrac{211}{5}$

Example 2: Solve the differential equation $\dfrac{dy}{dx}-\dfrac{y}{x}=2{{x}^{2}}$

Ans: Given equation is, $\dfrac{dy}{dx}-\dfrac{y}{x}=2{{x}^{2}}$

The above equation can also be written as,

$\dfrac{dy}{dx}+\left( -\dfrac{1}{x} \right)y=2{{x}^{2}}$

Here, $P=\dfrac{-1}{x}$ and $Q=2{{x}^{2}}$

By taking I.F. on both the sides, we get

$\Rightarrow {{e}^{\int{Pdx}}}={{e}^{\int{\dfrac{-1}{x}dx}}}={{e}^{-\log x}}$

$\Rightarrow {{e}^{\log {{x}^{-1}}}}$

$\Rightarrow {{x}^{-1}}=\dfrac{1}{x}$

$\dfrac{1}{x}\dfrac{dy}{dx}-\dfrac{1}{{{x}^{2}}}y=2x$

Now, Integrating both sides w.r.t. x, we get

$y\left( \dfrac{1}{x} \right)=\int{2x\,dx+c}$

$\dfrac{y}{x}={{x}^{2}}+c$

$y={{x}^{3}}+cx$

Solved problems of Previous Year Question

1. Solve: $\int {tan^32x sec^2x dx}$

Ans: Given $\int \tan^{3} 2 x \sec^{2} x dx$

The above equation can be written in the simplified form as,

$\int\left(\left(\sec^{2} 2 x-1\right) \sec^{2} x \times \tan^{2} x\right) dx$

$\Rightarrow \int \sec^{3} 2 x \tan^{2} x dx-\int \sec^{2} x \tan^{2} x dx$ —(i)

Taking $\int \sec^{3} 2 x \tan^{2} x dx$

Consider, $\sec 2 x=t$

$\Rightarrow \sec 2 x \tan 2 x=\dfrac{dt}{2}$ then it reduces to

On substituting we get $\dfrac{1}{2} \int {t}^{2} \mathrm{dt}=\dfrac{t^3}{6}$

As we have considered $\sec 2 x=t$ on replacing the value we get,

$\Rightarrow \dfrac{\sec^{3} 2 x}{6}$

From (i), $\int \sec^{3} 2 x \tan^{2} x dx-\int \sec 2 x \tan^{2} x dx$

$\Rightarrow \dfrac{\sec^{3} 2 x}{6}-\dfrac{\sec 2 x}{2}+c$

Trick used: Considering $\sec 2 x=t$, 

Then differentiate the above equation $\sec 2 x \tan 2 x dx=\dfrac{1}{2} dt$

2. If $f^\prime(x) = tan^{-1}(secx + tanx), - {\dfrac{\pi}{2}} < x < {\dfrac{\pi}{2}}$,

and $f(0) = 0$, then $ƒ(1)$ is equal to :

Ans: $f^{\prime}(x)=\tan^{-1}(\sec x+\tan x)$

$\Rightarrow f^{\prime}(x) = \tan^{-1}\left(\dfrac{1 + \sin x}{\cos x}\right) = \tan^{-1}\left(\dfrac{1 + \tan \dfrac{x}{2}}{1 - \tan \dfrac{x}{2}}\right)$

$\Rightarrow \tan^{-1}\left(\tan \left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\right)$

As, $-\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$

$\therefore 0 < \dfrac{\pi}{4} + \dfrac{x}{2} < \dfrac{\pi}{2}$

$\therefore f^{\prime}(x)=\dfrac{\pi}{4}+\dfrac{x}{2}$

because, $ f(0)=0 \Rightarrow c=0$

$\Rightarrow f(x)=\dfrac{\pi}{4} x+\dfrac{x^{2}}{4}+c$

$\Rightarrow \dfrac{x^{2}}{4}$

$\Rightarrow \dfrac{\pi+1}{4}$

3. If $\int {{\dfrac{{\cos x - \sin x}}{{\sqrt {8 - \sin 2x}}}}} dx = a{\sin ^{ - 1}}\left( {{\dfrac{{\sin x + \cos x}}{b}}} \right) + c$, where c is a constant of integration, then the ordered pair (a, b) is equal to

Ans: Given, $\int {{\dfrac{{\cos x - \sin x}}{{\sqrt {8 - \sin 2x}}}}} dx$

Write $\sin 2 x=1+\sin 2 x-1$

$\Rightarrow \int \dfrac{\cos x-\sin x}{\sqrt{8-[1+\sin 2 x-1]}} dx$

$\Rightarrow \int \dfrac{\cos x-\sin x}{\sqrt{8-\left[\sin ^{2} x+\cos ^{2} x+2 \sin x \cos x-1\right]}} dx$

$\Rightarrow \int \dfrac{\cos x-\sin x}{\sqrt{8-\left[(\sin x+\cos x)^{2}-1\right]}} dx$

$\Rightarrow \int \dfrac{\cos x-\sin x}{\sqrt{9-(\sin x+\cos x)^{2}}} dx$

Put $\sin x+\cos x=t$

$\Rightarrow(\cos x-\sin x) dx=dt$

$\Rightarrow \int \dfrac{dt}{\sqrt{9-(t)^{2}}}$

$\Rightarrow \sin ^{-1}\left(\dfrac{t}{3}\right)+C$

$\Rightarrow \sin ^{-1}\left(\dfrac{\sin x+\cos x}{3}\right)+C$

$\therefore$ $a=1$ and $b=3$

Practice Problems

1. If $\int {{x^5}} {e^{ - {x^2}}}dx = g\left( x \right){e^{ - {x^2}}} + c$, where c is a constant of integration, then $g(–1)$ is equal to :

Ans: $-\dfrac{5}{2}$

Hint: Consider $x^2=t$ and integrate, then substitute for $g(-1)$

2. Integrate $\int \dfrac{2 x^{3}-1}{x^{4}+x} dx$

Ans: $\ln \left(x^{3}+1\right)-\ln x+c$

Conclusion

In Integral Calculus, you should know all of the basic formulas for integration and differentiation, as well as the standard formulas for integration and differentiation. The fundamental theorems, Properties of definite integrals, Integration by Substitution, Integration by Parts and Integration by Partial Fractions.