




How Does a Magnetic Field Affect a Moving Charge?
The study of the effect of a magnetic field on a charge is fundamental in electromagnetism. When an electric charge moves through a magnetic field, it experiences a force that is perpendicular to both its velocity and the magnetic field direction. This interaction is crucial in understanding various physical phenomena and is essential for JEE Main preparation.
Definition and Properties of a Magnetic Field
A magnetic field is a region in which a moving electric charge or magnetic material experiences a force due to magnetism. The strength and direction of the magnetic field are represented by the vector $\vec{B}$, measured in tesla (T), and its influence is significant for moving charges.
Electric currents, as well as magnetic materials, can generate a magnetic field. The properties of the field can be analyzed using field lines and associated with other electromagnetic phenomena. For further details on related topics, refer to Electric Field Lines and Properties.
Moving Charge in a Magnetic Field
A moving electric charge in a magnetic field is subject to a force. This force depends upon the magnitude of the charge, the velocity of the charge, the strength of the magnetic field, and the angle between velocity and field direction.
The mathematical expression for the magnetic force $\vec{F}_m$ on a moving charge $q$ with velocity $\vec{v}$ in a magnetic field $\vec{B}$ is given by:
$\vec{F}_m = q (\vec{v} \times \vec{B})$
The magnitude of the force is:
$F_m = q v B \sin\theta$
Here, $\theta$ is the angle between $\vec{v}$ and $\vec{B}$. The force is maximized when the angle is $90^\circ$ and becomes zero when the directions are parallel or antiparallel.
Direction of Magnetic Force: Right Hand Rule
The direction of the magnetic force on a positive moving charge is given by the right hand rule. Point the thumb in the direction of velocity $\vec{v}$, the fingers in the direction of the magnetic field $\vec{B}$, and the force is directed perpendicular to the palm.
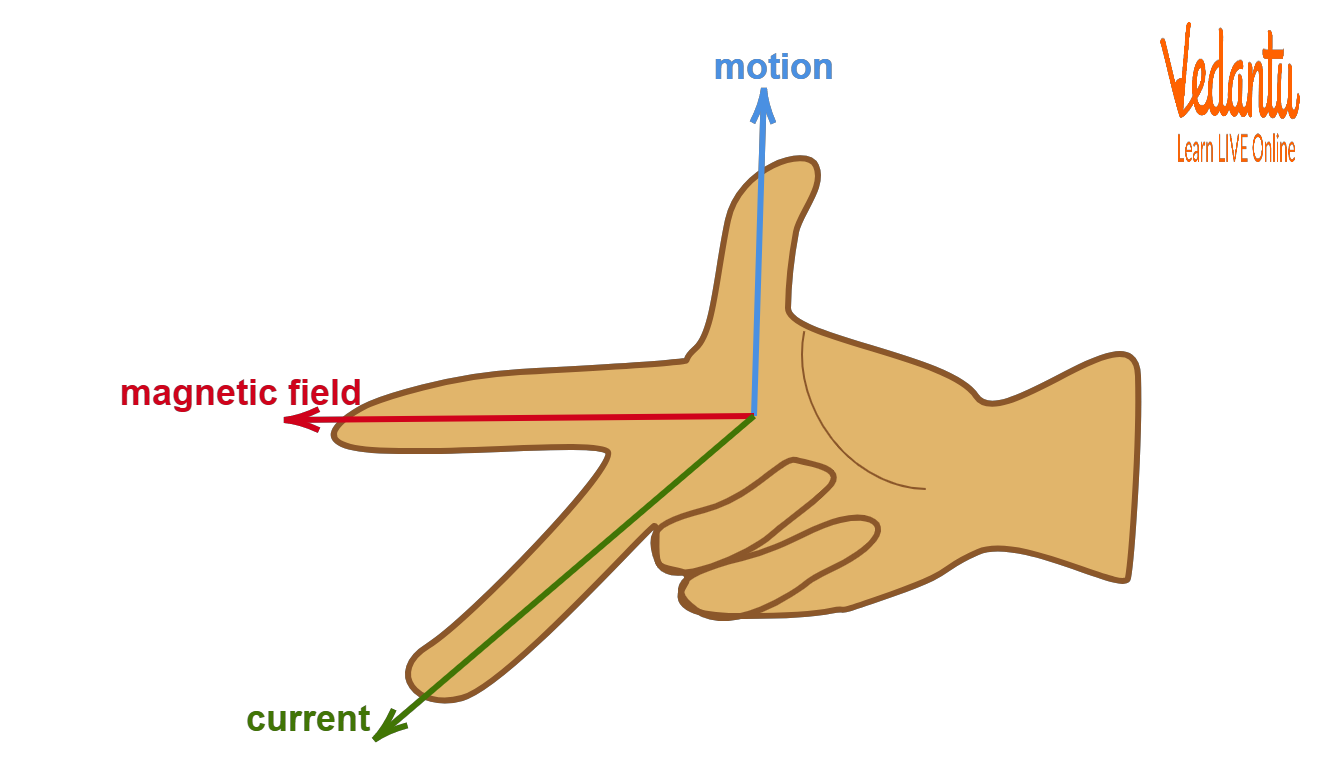
For negative charges, the force direction is opposite to that indicated by the right hand rule. This geometric relationship ensures that the force always acts perpendicular to both the magnetic field and velocity vectors.
Physical Significance and Effects
The magnetic force on a charged particle does not perform work, as it always acts perpendicular to the particle's velocity. Therefore, the speed of the particle remains unchanged, and only its direction changes. The trajectory becomes curved, depending on initial conditions.
This property leads to circular or helical paths for charged particles in uniform magnetic fields. Applications include cyclotron motion and devices like mass spectrometers. To explore more on electromagnetic phenomena, refer to Electromagnetic Induction and Alternating Current Notes.
Units of Magnetic Field
The SI unit for magnetic field strength ($B$) is the tesla (T). The relationship can be derived from the force expression:
$B = \dfrac{F}{q v \sin\theta}$
| Unit | Relationship |
|---|---|
| Tesla (T) | $1\,\mathrm{T} = 1\,\mathrm{N}\,(\mathrm{A}^{-1}\,\mathrm{m}^{-1})$ |
| Gauss (G) | $1\,\mathrm{G} = 10^{-4}\,\mathrm{T}$ |
Lorentz Force: Combined Electric and Magnetic Fields
When a charge moves in the presence of both electric and magnetic fields, the total force is known as the Lorentz force. It is defined as:
$\vec{F} = q \vec{E} + q (\vec{v} \times \vec{B})$
The first term represents the force due to the electric field, while the second term is the magnetic force. This equation is fundamental in analyzing the motion of charges in electromagnetic fields.
Solved Example: Force on a Moving Charge
A particle of charge $2 \times 10^{-8}$ C moves with a velocity of $10\,\mathrm{m/s}$ perpendicular to a magnetic field of $4 \times 10^{-5}\,\mathrm{T}$. The force experienced is calculated using:
$F_m = q v B \sin\theta = 2 \times 10^{-8} \times 10 \times 4 \times 10^{-5} \times 1 = 8 \times 10^{-12}\,\mathrm{N}$
Factors Affecting Magnetic Force
- Magnitude of charge on the particle
- Velocity of the particle
- Strength of the magnetic field
- Angle between velocity and field direction
Types of Magnetic Materials: Magnetic Response
Materials respond to magnetic fields based on their atomic structure. Diamagnetism, paramagnetism, and ferromagnetism are common types, depending on electron arrangement and presence of unpaired electrons. Detailed discussion on magnetism and its types is available at Magnetic Effects of Current.
Applications and Importance
The force on a charge in a magnetic field is exploited in devices like cyclotrons, velocity selectors, and in experimental determination of charge sign. It is also essential in the study of electromagnetic induction, which can be explored further at Understanding Lenz's Law.
Current conduction in materials also depends on the response of charge carriers to magnetic fields. For foundational knowledge, see Current Electricity Overview.
Important Points on Charge in a Magnetic Field
- Magnetic force acts perpendicular to both velocity and field
- No work is done by magnetic force on the charge
- Direction of force is predicted by right hand rule
- Only moving charges experience force from magnetic field
- Force on negative charge is opposite to right hand rule direction
Summary Table: Charge in a Magnetic Field
| Quantity | Expression |
|---|---|
| Magnetic Force | $F_m = q v B \sin\theta$ |
| Direction (positive charge) | Right hand rule |
| Unit of $B$ | Tesla (T) |
| Effect on speed | No change |
Related Topics for Further Study
Advanced applications include analysis of electromagnetic waves and quantum effects in magnetic fields. For insights on electromagnetic scattering, refer to Rayleigh Scattering Explained.
FAQs on Understanding the Motion of a Charge in a Magnetic Field
1. What happens when a charge moves in a magnetic field?
A moving charge in a magnetic field experiences a force known as the Lorentz force. This force acts perpendicular to both the velocity of the charge and the direction of the magnetic field.
Key points:
- The direction of the force is given by the right-hand rule.
- This force can cause the charge to move in a circular or helical path.
- The magnitude of the force is F = qvB sinθ, where q is the charge, v is velocity, B is the magnetic field strength, and θ is the angle between v and B.
2. What is the formula for the force on a charged particle in a magnetic field?
The formula for the force on a charge in a magnetic field is F = qvB sinθ. This is known as the Lorentz force law.
- F: Force experienced by the charge (Newtons)
- q: Charge (Coulombs)
- v: Velocity of the particle (m/s)
- B: Magnetic field strength (Tesla)
- θ: Angle between velocity and magnetic field direction
3. Why does a charge move in a circular path in a uniform magnetic field?
A charge in a uniform magnetic field moves in a circular path due to the constant magnitude of the Lorentz force acting perpendicular to its velocity.
This force provides the necessary centripetal force.
- The magnetic force does not work on the charge, it only changes its direction.
- Radius of the circular path: r = mv/qB
- Path shape depends on the charge's initial velocity angle to the field.
4. What is the right-hand rule for a moving charge in a magnetic field?
The right-hand rule helps predict the direction of the force on a positive charge in a magnetic field.
Steps:
- Point your thumb in the direction of the charge's velocity (v).
- Point your fingers in the direction of the magnetic field (B).
- The force (F) comes out of your palm — this is the force direction.
5. What is the motion of a charged particle in a magnetic field if velocity is parallel to the field?
If a charged particle's velocity is parallel to the magnetic field, it moves unaffected and continues in a straight line.
- No magnetic force acts since sinθ = 0.
- The particle's speed and direction remain unchanged.
- There is no change in kinetic energy or path shape.
6. What factors affect the force experienced by a charge in a magnetic field?
The force on a charge in a magnetic field depends on several factors:
- The magnitude of the charge (q)
- The speed of the particle (v)
- The strength of the magnetic field (B)
- The angle between velocity and field (θ)
7. How do you determine the direction of motion for a negative charge in a magnetic field?
For a negative charge, the direction of the force in a magnetic field is opposite to that given by the right-hand rule.
- Use the right-hand rule for a positive charge.
- Reverse the direction for negative charge (like an electron).
- The resulting force will curve the path accordingly.
8. What real-life examples demonstrate the effect of magnetic fields on moving charges?
Many real-life applications rely on the effect of magnetic fields on moving charges.
Examples include:
- Cyclotrons and synchrotrons (particle accelerators)
- Mass spectrometers
- The operation of CRT televisions and oscilloscopes
- Electric motors and generators
9. What is the significance of the angle θ in the formula F = qvB sinθ?
The angle θ determines how much of the velocity is perpendicular to the magnetic field and thus how strong the force is.
- If θ = 0°, sinθ = 0: The force is zero.
- If θ = 90°, sinθ = 1: The force is maximum.
- For other angles, the force is proportional to sinθ.
10. What is the path of a charged particle if it enters a magnetic field at an angle (not exactly parallel or perpendicular)?
A charged particle entering a magnetic field at an angle follows a helical (spiral) path.
- The velocity splits into parallel and perpendicular components.
- The parallel component remains unchanged.
- The perpendicular component causes circular motion.
- This results in a spiral or helix along the direction of the magnetic field.
































