Answer
Verified405k+ views
Hint: First draw the circuit diagram of the meter bridge. Then, try to figure out the null point of the Galvanometer and continue this with variable resistance. Now find the unknown resistance with the help of the Wheatstone bridge principle. The Wheatstone bridge works on the principle of null deflection, that is in normal condition the ratio of their resistance are unbalanced and current passes through it but in the other case when the galvanometer does not show any deflection the ratio of resistances is same and they get nullified and thus no current flows through it.
Complete step by step answer:
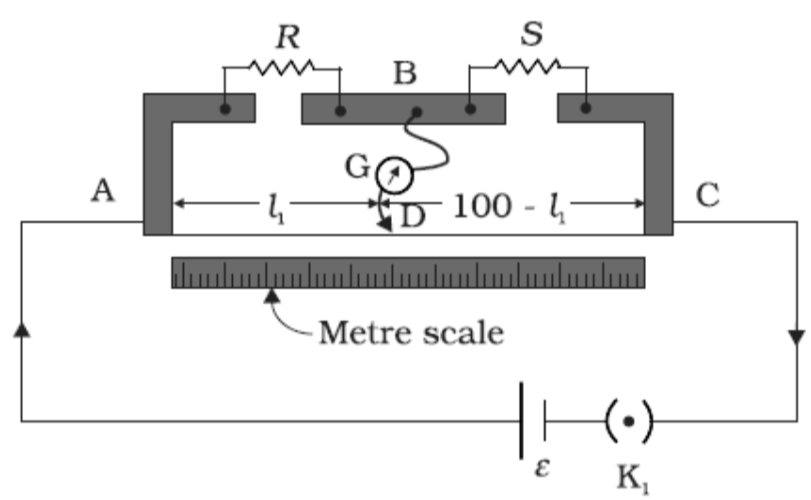
Above is the diagram of a meter bridge in which, R and S are two resistance, where R is a resistance box with variable resistance and S is a fixed resistance(this resistance is made up of the wire whose resistance is unknown). B, A, and C are metallic plates G is a galvanometer which is connected at point B with which a jockey D is connected, the meter scale is a 1 m scale divided into 100 divisions, K$_{1}$ is the key, and $\xi $ is a battery that is inside the circuit.
Now let us consider that ${{l}_{1}}$ is the length where the galvanometer shows zero deflections,
Therefore ${{l}_{2}}=100-{{l}_{1}}$ .
At first, the key K$_{1}$ is closed to pass a current and we are also choosing a suitable resistance R in the resistance box.
Then the jockey is tapped along the wire to locate the null point that is the point where the galvanometer shows zero deflection. The bridge is then said to be balanced.
And after that by the principle of Wheatstone bridge.
\[\dfrac{R}{{{l}_{1}}}=\dfrac{S}{{{l}_{2}}}\] ,
\[S=\dfrac{R\times {{l}_{2}}}{{{l}_{1}}}\],
Therefore, by this formula, we can find the unknown resistance of the wire.
As R is a known value so unknown resistance S can be calculated.
Note: We have to locate the exact zero point to apply the Wheatstone bridge principle, sometimes terminal error occurs that is the terminal of the devices get exchanged, check all the connections properly, and after doing the observation of one resistance switch of the circuit because if the wire gets heated up too much resistance will increase.
Complete step by step answer:
Above is the diagram of a meter bridge in which, R and S are two resistance, where R is a resistance box with variable resistance and S is a fixed resistance(this resistance is made up of the wire whose resistance is unknown). B, A, and C are metallic plates G is a galvanometer which is connected at point B with which a jockey D is connected, the meter scale is a 1 m scale divided into 100 divisions, K$_{1}$ is the key, and $\xi $ is a battery that is inside the circuit.
Now let us consider that ${{l}_{1}}$ is the length where the galvanometer shows zero deflections,
Therefore ${{l}_{2}}=100-{{l}_{1}}$ .
At first, the key K$_{1}$ is closed to pass a current and we are also choosing a suitable resistance R in the resistance box.
Then the jockey is tapped along the wire to locate the null point that is the point where the galvanometer shows zero deflection. The bridge is then said to be balanced.
And after that by the principle of Wheatstone bridge.
\[\dfrac{R}{{{l}_{1}}}=\dfrac{S}{{{l}_{2}}}\] ,
\[S=\dfrac{R\times {{l}_{2}}}{{{l}_{1}}}\],
Therefore, by this formula, we can find the unknown resistance of the wire.
As R is a known value so unknown resistance S can be calculated.
Note: We have to locate the exact zero point to apply the Wheatstone bridge principle, sometimes terminal error occurs that is the terminal of the devices get exchanged, check all the connections properly, and after doing the observation of one resistance switch of the circuit because if the wire gets heated up too much resistance will increase.