Question

Using integration, find the area of the region bounded by the line \[2y+x=8\], the x-axis, and the ordinates \[x=2\] and \[x=4\]

Answer 1

Hint: In this question, we first need to plot the given line within the given ordinates. After that you will find an enclosed region then we are going to find the area of that bounded region. We know that, area under the curve is calculated by integrating the curve over x as follows: $\int\limits_{a}^{b}{ydx}$. Using this concept, we are going to integrate \[y=\dfrac{8-x}{2}\] with respect to x and the limits of x over which integration will occur is from $x=2\text{ to }x=4$. The result of this integration is the area of the bounded region.

Complete step by step answer:
Now, let us first plot the given line in the question within the ordinates

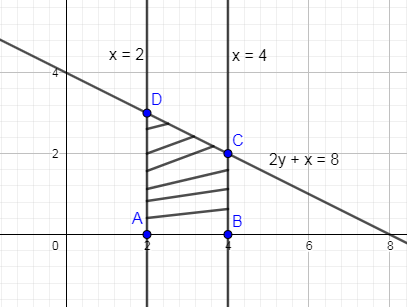
Here, we need to find the area of the shaded region which we have shown by the area inside ABCD.
 As we already know from the applications of integration that the space occupied by the curve along with the axis, under the given condition is called area of bounded region.
The area bounded by the curve \[y=f\left( x \right)\] above the x-axis and between the lines \[x=a,x=b\]is given by
\[\int\limits_{a}^{b}{y}dx=\int\limits_{a}^{b}{f\left( x \right)dx}\]
Now, from the given line in the question we have
\[\Rightarrow 2y+x=8\]
Now, this can also be written as
\[\Rightarrow y=\dfrac{-x}{2}+4\]
Now, the area of the shaded region can be found by integrating the above line equation within the given ordinates
\[\Rightarrow \int\limits_{a}^{b}{y}dx\]
Now, from the given conditions in the question we have
\[\Rightarrow y=\dfrac{-x}{2}+4,a=2,b=4\]
Now, on substituting these respective values in the above formula we get,
\[\Rightarrow \int\limits_{2}^{4}{\left( \dfrac{-x}{2}+4 \right)}dx\]
As we already know from the properties of integration that
\[\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}\]
Now, on integrating the above expression using the formula we get,
\[\Rightarrow \left( \dfrac{-{{x}^{2}}}{4}+4x \right)_{2}^{4}\]
Now, on substituting the values and simplifying it further we get,
\[\Rightarrow \left( \dfrac{-{{4}^{2}}}{4}+4\times 4-\left[ \dfrac{-{{2}^{2}}}{4}+4\times 2 \right] \right)\]
Now, this can be further written in the simplified form as
\[\Rightarrow \left( \dfrac{-16}{4}+16-\left[ \dfrac{-4}{4}+8 \right] \right)\]
Now, on further simplification we get,
\[\Rightarrow 12-7\]
\[\Rightarrow 5\]

Hence, the area of the region is 5.

Note: Instead of integrating with respect to x in the given ordinates we can also calculate it by integrating it with respect to y and find the value of y for the given ordinate values to integrate within those limits. Both the methods give the same result.
It is important to note that while calculating we should not consider wrong limits or neglect any of the terms while integrating because neglecting any of the terms or calculation errors changes the result.