Question

Using Gauss’s law obtain the expression for the electric field due to the uniformly charged thin spherical shell of radius $R$ at a point outside the shell. Draw a graph showing the variation of electric field with $r$, for $r > R$ and $r < R$.

Answer 1

Hint A uniformly charged sphere is spherically symmetric i.e. all points around the sphere are identical. Therefore, choose a spherical Gaussian surface whose radius is equal to the distance$r$ from the center of the sphere.
Formula used: $\oint {\vec E \cdot d\vec A} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _0}}}$ where $\vec E$ is the electric field vector, $d\vec A$ is the infinitesimal area vector, ${Q_{enc}}$ is the charge enclosed in the Gaussian surface and ${\varepsilon _0}$ is the permittivity of free space, $\oint {\vec E \cdot d\vec A} $ is the total flux going through the Gaussian surface.

Complete step by step answer

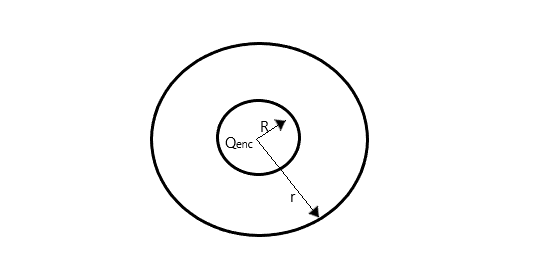
Gauss law allows us to easily find the electric field of a charge distribution by taking advantage of a possible symmetry in its arrangement. From integral form of Gauss law, we have
$\Rightarrow \oint {\vec E \cdot d\vec A} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _0}}}$
For a uniform spherical charge, the equation becomes
$\Rightarrow E \times A = \dfrac{{{Q_{enc}}}}{{{\varepsilon _0}}}$ because the electric fields flowing through every infinitesimal area of our Gaussian surface are equal.
Then,
$\Rightarrow E \times 4\pi {r^2} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _0}}}$ (since $A = 4\pi {r^2}$)
Rearranging for $E$, we get
$\Rightarrow E = \dfrac{{{Q_{enc}}}}{{4\pi {\varepsilon _0}{r^2}}}$
$\therefore E \propto \dfrac{1}{{{r^2}}}$
The electric field for a uniformly charged thin spherical shell at radius $r < R$ is zero (since there would be no charge enclosed).
Hence, the graph of electric field with distance is as shown below.

Note
For $r < R$ we said that this is due to the fact that there would be no charged enclosed. For further understanding consider the constant form of Gauss’s law
$\Rightarrow E \times A = \dfrac{{{Q_{enc}}}}{{{\varepsilon _0}}}$
For $r < R$, we pick a Gaussian surface that is inside the spherical shell. Since the charges are distributed around the shell, the charge enclosed by the Gaussian surface is zero, i.e. $\Rightarrow {Q_{enc}} = 0$. Hence, from
$\Rightarrow E \times A = \dfrac{{{Q_{enc}}}}{{{\varepsilon _0}}} $
$\Rightarrow E = 0 $
Also, $E$ is maximum at $r = R$ because ${Q_{enc}} = \sigma 4\pi {R^2}$ where $\sigma $ is the surface charge density. Thus, from $E = \dfrac{{{Q_{enc}}}}{{4\pi {\varepsilon _0}{r^2}}}$ we replace ${Q_{enc}}$ as $\sigma 4\pi {R^2}$. Then, we have
$\Rightarrow E = \dfrac{{\sigma 4\pi {R^2}}}{{4\pi {\varepsilon _0}{r^2}}}$.
For $r = R$,
$\Rightarrow E = \dfrac{\sigma }{{{\varepsilon _0}}}$